模型背后的数学,从加性假设到伪逆矩阵
技术免责声明:可以推导出一个不需要正态假设的模型。我们将选择这条路线,因为它足够简单易懂,并且通过假设模型输出服从正态分布,我们可以推断出预测的不确定性。
本文旨在为那些已经了解线性回归是什么(可能使用过一两次)并希望更系统地了解背后数学原理的人提供帮助。
在接下来的内容中,可能需要一些基本概率(概率分布、联合概率、互斥事件)、线性代数和统计学的背景知识才能充分理解。废话不多说,我们开始吧:
机器学习世界充满了惊人的联系:指数家族、正则化和先验信念、KNN和SVM、最大似然和信息论——一切都相互关联!(我喜欢黑暗)。这次我们将讨论如何推导出指数家族的另一个成员:线性回归模型,并在此过程中看到均方误差损失的理论基础。与任何回归模型一样,我们可以使用它来预测数值连续目标。它是一个简单但强大的模型,也是统计推断和实验设计中的工具之一。但我们只关注它作为预测工具的使用,没有繁琐的推断(更不要说因果)内容。
好的,我们开始吧。我们想要根据某些东西来预测其他东西。我们将预测的东西称为y,其他东西称为x。作为一个具体的例子,我提供以下玩具情景:你是一家银行的信贷分析师,你有兴趣自动找出银行客户的正确信贷额度。你还恰好有一份关于过去客户以及他们的特征(如人口统计信息、过去的信贷表现、收入等)和批准的信贷额度(预测的东西)的数据集。
所以我们有一个很好的想法,写下一个模型来解释信贷额度与这些可用特征之间的关系,模型的主要假设是每个特征以加性方式对观察到的输出做出贡献。由于信贷方面只是一个激励(和人为的)例子,让我们回到我们纯数学的世界,我们的模型变成了这样:
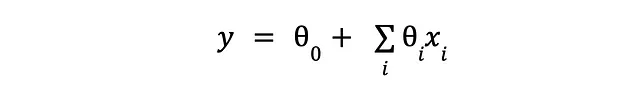
我们仍然有预测的东西(y)和我们用来预测它的其他东西(x)。我们承认某种噪音是不可避免的(无论是由于测量不完美还是我们自己的盲目),我们唯一能做的就是假设我们观察到的数据背后的模型是随机的。这样做的结果是,对于相同的输入,我们可能会看到稍微不同的输出,因此我们“困在”以输入(x)为条件的输出(y)的概率分布中:
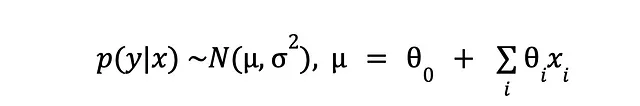
每个y中的数据点都被一个小钟形曲线所取代,其均值位于y的观察值中,并且具有某个我们暂时不关心的方差。然后我们的小模型将代替分布的均值。
假设所有这些钟形曲线实际上都是正态分布,它们的均值(y中的数据点)彼此独立,观察到数据集的(联合)概率为
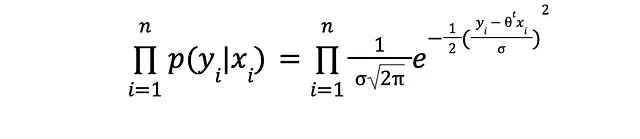
对数和一些代数来拯救:
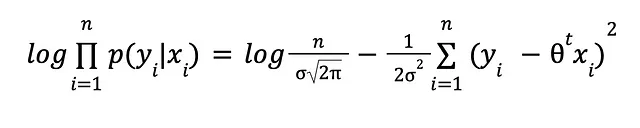
对数是很酷的,不是吗?对数将乘法转换为加法,除法转换为减法,乘方转换为乘法。从代数和数值的角度来看,非常方便。摆脱常数项,对于这个问题来说是无关紧要的,我们得到了以下的最大似然问题:
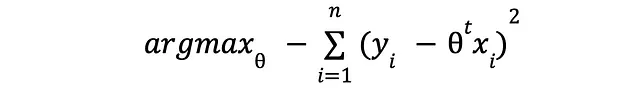
嗯,这与下面的表达式相同
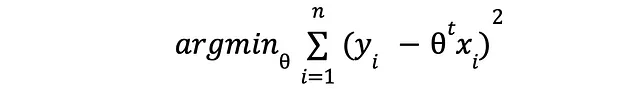
我们将要最小化的表达式与著名的均方误差(Mean Square Error)损失非常相似。事实上,从优化的角度来看,它们是等效的。
那么现在怎么办?这个最小化问题可以通过求导来解决。我们将利用损失是二次的事实,这意味着是凸的,也就是说有一个全局最小值;我们可以对其求导,将导数设为零,然后解出 theta。通过这样做,我们将找到使得损失的导数为零的参数 theta 的值。为什么呢?因为在导数为零的点,损失达到了最小值。
为了使一切都变得简单些,让我们用向量表示法来表达损失:
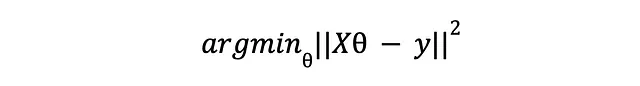
在这里,X 是一个 NxM 的矩阵,表示我们的整个数据集,其中包含 N 个示例和 M 个特征,y 是一个包含每个训练示例的预期响应的向量。对其进行求导并将其设为零,我们得到
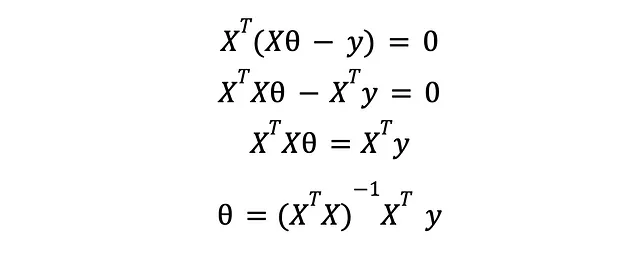
在这里,你已经得到了,我们将原始机器学习问题转化为的优化问题的解决方案。如果你继续将这些参数值插入到你的模型中,你将得到一个经过训练的机器学习模型,可以使用一些保留数据集(或者通过交叉验证)进行评估。
如果你认为最终的表达式看起来很像一个线性系统的解决方案,
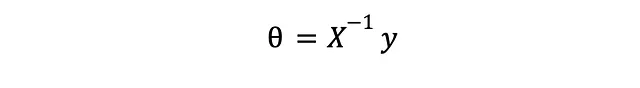
那是因为它确实如此。额外的部分来自于我们的问题要等价于一个普通线性系统,我们需要有相等数量的特征和训练示例,这样我们才能求解矩阵 X 的逆。由于这种情况很少出现,我们只能希望得到一个“最佳拟合”解决方案 – 在某种意义上是最佳的 – 借助于 X 的摩尔-彭罗斯伪逆,它是对好老的逆矩阵的一种推广。相关的维基百科条目是一篇有趣的阅读。
对正则化的小探索
从现在开始,我假设你可能在某个地方听过“正则化”这个术语,也许你知道它是什么。无论如何,我告诉你我是如何理解它的:正则化是指对模型进行的任何操作,以使其在样本外的性能更好,但以牺牲样本内性能为代价。为什么会有这样的事情?因为最终,在样本外(即现实生活中)的性能才是最重要的 – 没有人会关心你的训练误差有多低,或者你在训练集上的 AUC 有多惊人,除非你的模型在生产中表现得相对良好。我们发现,如果我们不小心,我们会遇到所谓的过拟合问题,即模型将训练集完全记住,直到噪声,可能对样本外预测变得无用。我们还知道,模型复杂度和样本外性能之间存在权衡(Vapnik 的统计学习理论),而正则化可以被看作是一种试图控制模型复杂度,以期达到更好泛化能力的尝试(这里的泛化是指样本外性能的另一个名称)。
正则化可以采用多种形式,但是在本文中,我们只讨论一种常用于线性回归模型的方法。记得我说过,通过正则化,我们试图控制复杂性,对吧?好吧,不想要的复杂性主要通过两种方式产生:1. 太多的输入特征和2. 对应的θ值过大。事实证明,L2正则化可以同时解决这两个问题。记得我们的损失函数吗?
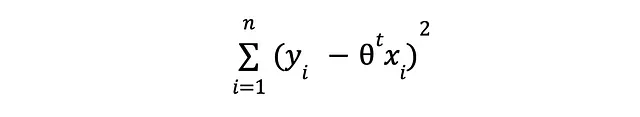
我们只关心最小化预测值与观测值y之间的平方差异,而不考虑其他任何因素。这种短视的关注可能会存在问题,因为你原则上可以通过不断添加特征来使误差变得微不足道,即使这些额外的特征与我们试图学习的信号毫无关系。如果我们对问题相关的事物有完美的了解,我们就不会包含无用的特征!(公平地说,我们一开始就不会使用机器学习,但我岔开了话题)。为了弥补我们的无知并减轻引入不必要的复杂性的风险,我们将在损失函数中添加一个额外的项:
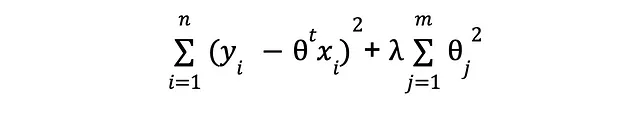
你可能会问,这是什么作用。我告诉你——我们刚刚引入了一种鼓励将参数的大小尽可能接近零的激励机制。换句话说,我们希望将复杂性保持在最低限度。现在,我们不仅有一个目标(最小化预测误差),还有一个目标(最小化复杂性),解决整体问题的解决方案将需要平衡两者。通过那个闪亮的新lambda系数,我们可以影响这个平衡的样子:它越大,我们就越重视低复杂性目标。
说了这么多。让我们看看额外的项对最优θ值的影响。向量化形式的新损失函数为
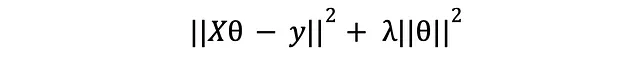
对其进行导数运算,令其等于零并解出θ:
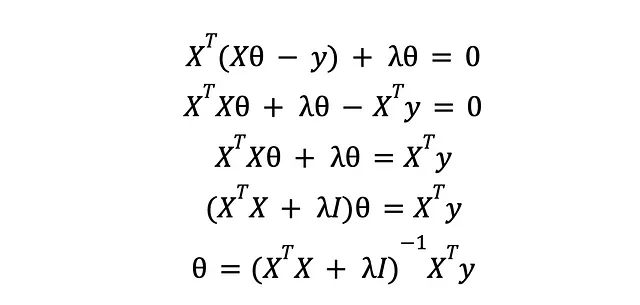
结果表明,新解与以前的解并没有太大的区别。我们得到了一个额外的对角矩阵,它将通过添加一些“抖动”来处理可能阻止我们对XTX矩阵进行求逆的秩问题。这揭示了引入不必要的复杂性的另一种方式:共线特征,即线性变换(缩放和平移版本)的特征。对于线性回归来说,两个共线特征是相同的特征,只计算为一列,并且额外的特征不会添加任何新信息来帮助训练我们的模型;从而使XTX矩阵秩亏损,即不可逆。通过正则化,在XTX的每一行中,不同的列都受到lambda(抖动)的影响,阻止了任何可能的共线性,并使其具有完全秩。我们可以看到,随机添加垃圾作为预测变量实际上可能会破坏整个学习过程。幸运的是,正则化来拯救这一天(请不要误解我对正则化的赞扬是对在选择预测变量时粗心大意的邀请)。
所以,现在你有了一个可以使用的正则化线性回归模型。我们接下来怎么做呢?嗯,你可以深入探讨正则化编码关于参数空间的先验信念,揭示它与贝叶斯推断的联系。或者你可以进一步探讨它与支持向量机以及最终与非参数模型(如KNN)的联系。此外,你还可以思考一下线性回归和逻辑回归的所有那些花哨的梯度看起来非常相似的事实。放心,我将在未来的文章中涉及这些主题!