
大数定律的有趣之处在于它所没有说的和它所说的一样
1966年8月24日,一位才华横溢的剧作家汤姆·斯托帕德在苏格兰的爱丁堡上演了一出戏剧。这出戏有一个奇特的标题,《罗森克朗兹与吉尔登斯特恩已死》。剧中的主要角色罗森克朗兹和吉尔登斯特恩是莎士比亚名作《哈姆雷特》中的童年朋友。剧开场时,吉尔登斯特恩一再抛硬币,结果都是正面。每次结果都使吉尔登斯特恩的钱袋减轻,罗森克朗兹的钱袋则加重。随着连续不断的正面出现,吉尔登斯特恩开始担心。他担心自己是否暗地里希望每个硬币都出现正面,作为对某个早已被遗忘的罪行的自我惩罚。或者如果时间在第一次抛硬币后停止,他和罗森克朗兹正在一次又一次地经历相同的结果。
斯托帕德出色地展示了概率法则如何融入我们对世界的看法,融入我们的期望感,融入人类思维的纤维。当第92次抛硬币的结果也是正面时,吉尔登斯特恩问自己和罗森克朗兹是否处于一个不受概率法则支配的不自然现实之中。
吉尔登斯特恩的担忧当然是没有根据的。诚然,连续得到92次正面的可能性是难以想象的小。事实上,这是一个小数点后面跟着28个零和2。吉尔登斯特恩更有可能被陨石砸到头上。
吉尔登斯特恩只需要第二天回来抛另一组92次硬币,结果几乎肯定会大不相同。如果他每天都按照这个例程进行,他会发现大多数时候正面的数量与反面的数量差不多。吉尔登斯特恩正在体验到我们宇宙中一个迷人的行为,被称为大数定律。
以通俗的英语解释的大数定律
大数定律有两种形式:弱大数定律和强大数定律。弱大数定律可能更直观、更容易理解,但也容易被误解。本文将介绍弱版本,将强版本的讨论留到以后的文章中。
弱大数定律关注的是样本均值和总体均值之间的关系。我将用平实的文字解释它的含义:
假设你从总体中随机抽取一定数量的样本,比如100个。顺便说一下,“样本大小”这个术语,请在心中记下。样本的“大小”是这个定律的马戏团团长,是这个定律的至高无上者。现在计算这个样本的均值并将其放在一边。接下来,重复这个过程很多次。你将得到一组不完美的均值。这些均值是不完美的,因为它们与真实的总体均值之间总会有一个“差距”,一个偏差。假设你可以接受某种偏差。如果你从这组均值中随机选择一个样本均值,那么样本均值与总体均值之间的绝对差异超过你的容忍度的概率将会收缩到零。
弱大数定律说,随着样本大小增加到无限大或接近总体大小,这种超过你选择的容忍水平的偏差的概率将会趋近于零。
无论你选择的容忍水平有多小,当你抽取越来越大的样本集时,从这组样本中随机选择的均值超过这个容忍度的概率将会越来越小。
弱大数定律的现实世界例证
为了看到弱大数定律的工作原理,我们将通过一个例子来演示。为此,请允许我带您来到北大西洋东北部冷峻辽阔的海洋。
每天,爱尔兰政府都会发布一份从北东北大西洋表面获取的水温测量数据集。该数据集包含了数十万个按纬度和经度索引的表面水温测量值。例如,2023年6月21日的数据如下:
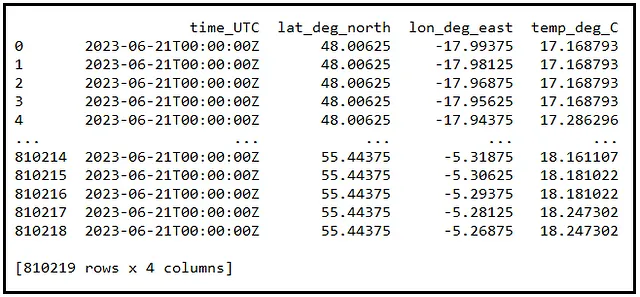
很难想象八十万个表面温度值是什么样子。因此,让我们创建一个散点图来可视化这些数据。我在下面展示了这个图。图中的空白区域代表了爱尔兰和英国。

作为一名统计学的学生,你将永远无法访问到“总体”。因此,如果我将这八十万个温度测量值视为“总体”,你对我进行严厉的指责是正确的。但请稍等片刻,你很快就会明白为什么在我们追求理解弱大数定律时,将这些数据视为“总体”会有所帮助。
那么,让我们假设这些数据是——咳咳——总体。这个总体中的810,219个位置的平均表面水温为17.25840摄氏度。17.25840只是810K温度测量值的平均值。我们将这个值指定为总体均值μ。请记住这个值。你将经常需要参考它。
现在假设你无法访问这810,219个值的总体。相反,你只能访问到从这个总体中随机抽取的20个样本位置。下面是一个这样的随机样本:
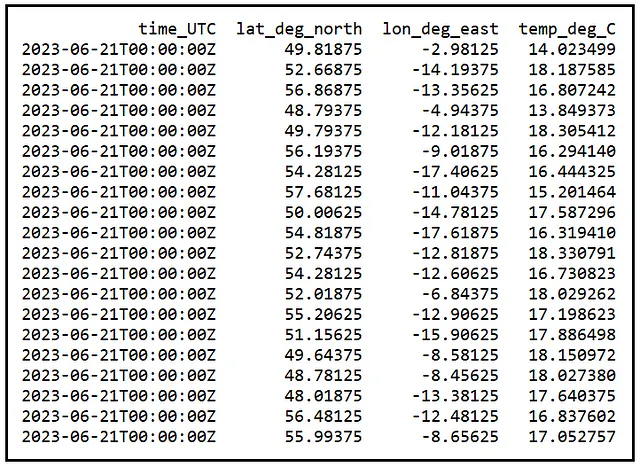
样本的平均温度是16.9452414摄氏度。这是我们的样本均值X_bar,计算如下:
X_bar = (X1 + X2 + X3 + … + X20) / 20
你可以轻松地从同一个总体中抽取第二个、第三个,甚至任意数量的大小为20的随机样本。以下是一些示例随机样本:
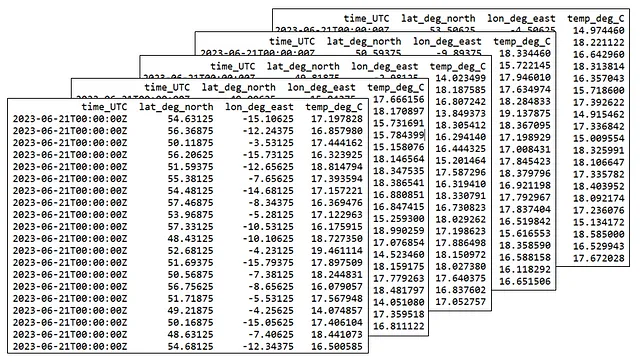
关于什么是随机样本的一个简短说明
在继续之前,让我们暂停一下,对随机样本的概念有一定的了解,这将更容易理解弱大数定律的工作原理。为了获得这个观点,我必须向你介绍赌场的老虎机:

上面展示的老虎机有三个插槽。每次你转动手臂,机器会从内部维护的图片总体(比如一系列水果图片的列表)中随机选择一张图片填充到每个插槽中。现在想象一台有20个插槽的老虎机,每个插槽命名为X1到X20。假设该机器被设计用于从810,219个温度测量值的总体中选择值。当你拉动手臂时,每个插槽——X1到X20——都会填充一个随机选择的值,选自810,219个值的总体。因此,X1至X20是可以分别保存总体中任意值的随机变量。它们共同形成了一个随机样本。换句话说,随机样本的每个元素本身就是一个随机变量。
X1到X20有一些有趣的特性:
- X1的取值与X2到X20的取值是独立的。对X2、X3、…、X20也是如此。因此X1到X20是独立的随机变量。
- 由于X1、X2、…、X20可以取自总体的任意值,它们的平均值是总体均值μ。使用期望的符号E(),我们可以将这个结果写成:E(X1) = E(X2) = … = E(X20) = μ。
- X1到X20有相同的概率分布。
因此,X1、X2、…、X20是独立同分布的随机变量。
…现在我们回到展示弱大数定律如何工作的内容
让我们计算这个包含20个元素的样本的平均值(表示为X_bar)并将其放在一边。现在让我们再次转动机器的手臂,然后弹出另一个包含20个元素的随机样本。我们将计算其平均值并将其放在一边。如果我们重复这个过程一千次,我们将计算出一千个样本均值。
这是通过这种方式计算的1000个样本均值的表格。我们将它们标记为X_bar_1到X_bar_1000:

现在仔细考虑以下陈述:
由于样本均值是从一个随机样本中计算出来的,样本均值本身也是一个随机变量。
此时,如果你正明智地点头并摸着下巴思考,那是非常正确的做法。意识到样本均值是一个随机变量是统计学中最深刻的领悟之一。
还要注意上面表格中的每个样本均值与总体均值μ相距一定距离。让我们绘制一个这些样本均值的直方图,看看它们如何在μ周围分布:
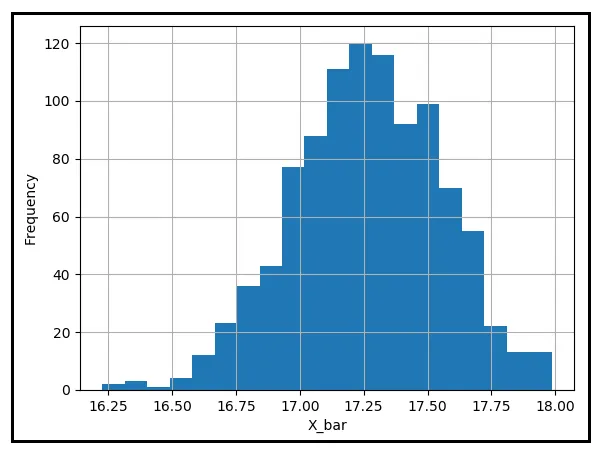
大多数样本均值似乎接近于17.25840摄氏度的总体均值。然而,也有一些样本均值与μ相距较远。假设你对这个距离的容忍度是0.25摄氏度。如果你把手伸进这桶里的1000个样本均值中,抓住任意一个距离你可及的均值并拿出来。这个均值与μ的绝对差值等于或大于0.25摄氏度的概率是多少?为了估计这个概率,你必须计算与μ至少相差0.25摄氏度的样本均值的数量,并将该数量除以1000。
在上表中,这个数量恰好是422,所以概率P(|X_bar — μ | ≥ 0.25)等于422/1000 = 0.422
让我们暂时放下这个概率。
现在重复上述所有步骤,但这次使用样本大小为100而不是20。所以你要做的是:抽取1000个大小为100的随机样本,计算每个样本的均值,保存所有这些均值,计算那些与μ相差至少0.25摄氏度的均值的数量,并将该数量除以1000。如果这听起来像大力士的劳动,那么你没错。所以请花一点时间喘口气。一旦你恢复过来,注意下面你为这些劳动得到的成果。
下面的表格包含了1000个随机样本的平均值,每个样本的大小为100:
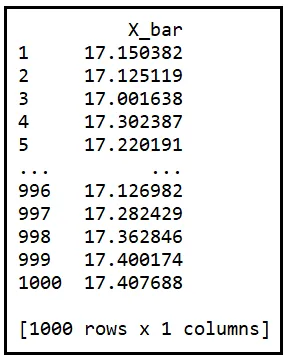
在这1000个均值中,有56个均值恰好偏离μ不超过0.25摄氏度。这给出了你遇到这样的均值的概率,即56/1000 = 0.056。这个概率明显小于之前样本大小只有20时计算得出的0.422。
如果你多次重复这个步骤序列,每次使用递增的不同样本大小,你将得到一张充满概率的表格。我已经为你完成了这个练习,从10逐步增加样本大小到490。以下是结果:
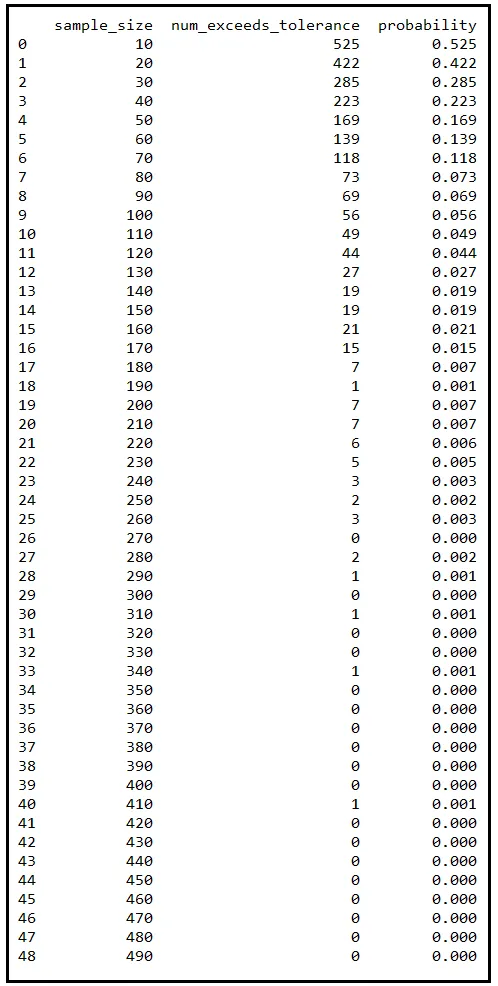
这个表格中的每一行都对应着从810219个温度测量结果的总体中随机抽取的1000个不同样本。 sample_size 列提及了这1000个样本的大小。一旦抽取完成,我计算了每个样本的均值,并计数了与μ相差至少0.25摄氏度的样本数。 num_exceeds_tolerance 列提及了这个计数。 probability 列是 num_exceeds_tolerance / sample_size。
注意随着样本大小的增加,这个计数迅速减少。相应的概率P(|X_bar — μ | ≥ 0.25)也是如此。当样本大小达到320时,概率已经衰减到零。它偶尔会增加到0.001,但这是因为我抽取了有限数量的样本。如果每次我抽取的样本量不是1000而是10000,不仅偶尔的增加将消失,概率的衰减也会变得更平滑。
下面的图表将 P(|X_bar — μ | ≥ 0.25) 与样本大小进行了绘制。它清晰地展示了随着样本大小的增长,概率将会降至零。
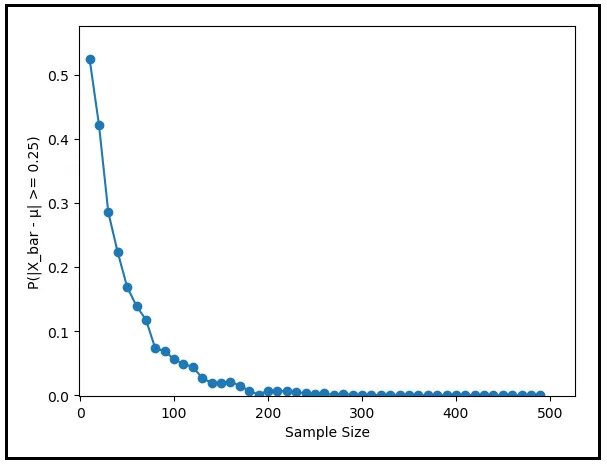
如果你选择了一个不同的公差(tolerance) —— 无论是更低还是更高的值,0.25摄氏度的情况将如何?概率是否会无论你选择的公差水平如何而衰减?下面的一系列图表说明了这个问题的答案。
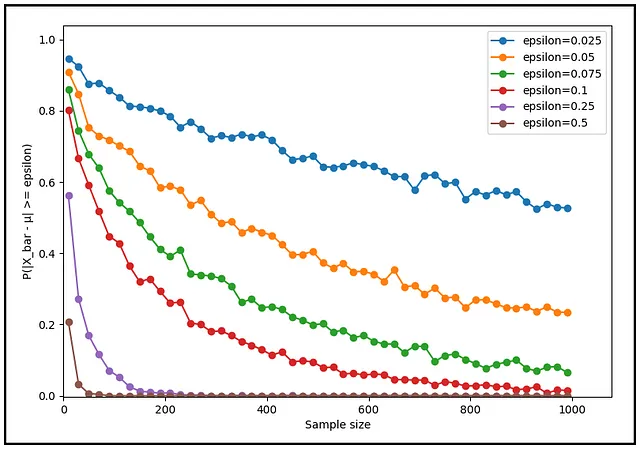
无论你选择多么严格、多么小的公差(ε),概率 P(|X_bar — μ | ≥ ε) 随着样本大小的增长总会趋近于零。这就是弱大数定律的实际效果。
弱大数定律的正式陈述
弱大数定律的行为可以正式陈述如下:
假设X1,X2,…,Xn是独立同分布的随机变量,它们共同构成了一个大小为n的随机样本。假设X_bar_n是这个样本的均值。假设还有E(X1) = E(X2) = … = E(Xn) = μ。那么对于任意非负实数ε,当样本的大小趋向于无穷大时,X_bar_n离μ至少ε的概率趋近于零。下面的精妙方程捕捉了这种行为:
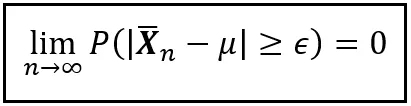
在这个定律的310年历史中,数学家已经能够逐渐放松X1到Xn独立同分布的要求,同时仍然保持这个定律的精神。
“概率收敛”原理、“plim”符号和用尽可能少的词表达重要观点的艺术
用概率作为运输方式以某个值收敛的特定方式称为概率收敛。一般来说,可以如下陈述:
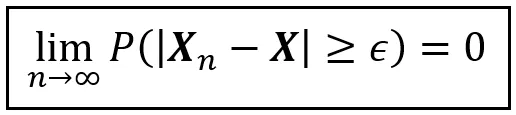
在上面的方程中,X_n和X是随机变量。ε是一个非负实数。该方程表明,当n趋向于无穷大时,X_n以概率收敛于X。
在统计学的广阔领域中,你会经常遇到一个安静谦逊的符号,叫做plim。它的发音是‘p lim’,或者‘plim’(像单词‘plum’但‘i’的发音),或概率极限。plim是一种简洁的表达方式,表示某个度量(如均值)以概率收敛到一个特定的值。利用plim,可以简洁地陈述弱大数定律如下:
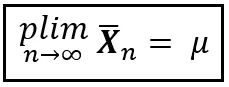
或者简单地表示为:
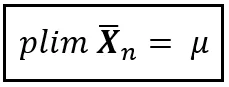
这种简洁的符号并不奇怪。数学家们喜欢简洁,就像蜜蜂喜欢花蜜一样。在传达深刻真理时,数学可能是最节约墨水的领域。在这个追求效率的领域中,plim占据了重要位置。你会很难找到一个比plim更简洁的概念,无论是用墨水还是电子。
但不用再苦苦挣扎了。如果plim简洁的美让你渴望更多,这里还有另一种可能更高效的符号,它传达的意义与plim相同:
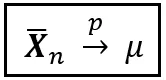
打破关于弱大数定律的一些迷思
在本文的开头,我提到弱大数定律之所以值得关注,是因为它所说的与它所不说的一样重要。让我解释一下我的意思。弱大数定律经常被误解为随着样本量增加,其均值趋近于总体均值或各种类似概念的意思。正如我们所看到的,这种关于弱大数定律的想法与现实没有任何关联。
事实上,让我们立即打破关于弱大数定律的几个迷思。
迷思1:随着样本量的增长,样本均值趋近于总体均值。
这可能是对弱大数定律最常见的误解。然而,弱大数定律并没有作出这样的断言。要理解其中的原因,请考虑以下情况:你已经成功地获得了一个非常大的样本。当你欣喜若狂地欣赏你的成就时,你也应该问自己以下问题:仅仅因为你的样本很大,它就一定是平衡的吗?什么阻止自然用一个包含大量偏差的巨大样本对你进行打击呢?答案是绝对没有!实际上,那不就是吉尔登斯坦在他连续92次正面的序列中发生的事情吗?毕竟,那是一个完全随机的样本!如果它碰巧有一个很大的偏差,那么尽管样本量很大,偏差将把样本均值推向远离真实总体值的地方。相反,一个小样本可能被证明是非常平衡的。关键是,随着样本量的增加,样本均值并不能保证忠实地接近总体均值。自然界并不提供这样不必要的保证。
迷思2:随着样本量的增加,样本的几乎所有属性——它的中位数、方差、标准差——都趋于相应的总体值。
这句话将两个迷思捆绑在一个方便携带的包裹中。首先,弱大数定律假定的是概率收敛,而不是值收敛。其次,弱大数定律仅适用于样本均值的概率收敛,而不适用于任何其他统计量的收敛。弱大数定律不涉及中位数、方差或标准差等其他测量的收敛。
如何知道弱大数定律是否适用?
陈述弱大数定律,甚至使用现实数据演示其工作是一回事。但是你如何确信它总是有效?是否存在某些情况下它会搅局,即样本均值根本不会以概率收敛到总体值?要知道这一点,你必须证明弱大数定律,并在此过程中准确定义适用它的条件。
弱大数定律有一个美味诱人的证明,其中之一是使用了无穷诱人的切比雪夫不等式。如果这引起了你的兴趣,请继续关注我下一篇关于弱大数定律证明的文章。
重温吉尔登斯坦
在没有消除我们的朋友吉尔登斯坦的担忧之前,离开这个话题将是不礼貌的。让我们对他所经历的结果有一个无可置疑地不太可能的认识。我们将使用伪随机生成器模拟投掷92个无偏硬币的行为。正面将编码为1,反面为0。我们将记录92次投掷的均值。均值是硬币正面朝上的次数的比例。我们将重复这个实验一万次,得到一万个92次投掷的均值,并绘制它们的频率分布。完成这个练习后,我们将得到以下类型的直方图图示:
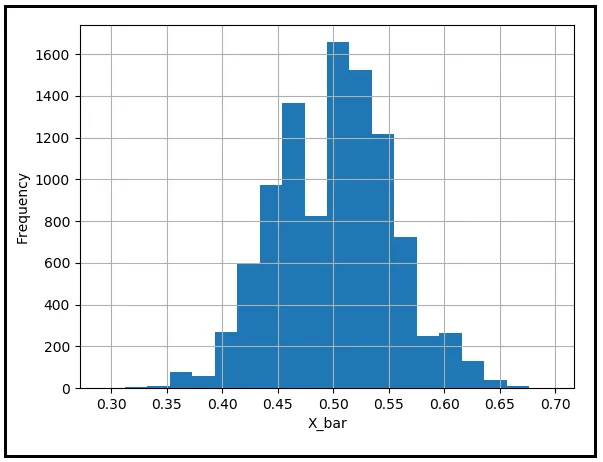
我们可以看到,大多数样本均值聚集在总体均值0.5附近。吉尔登斯坦的结果——连续得到92次正面朝上——是一个异常不太可能的结果。因此,这个结果的频率也非常小。但与吉尔登斯坦的担忧相反,这个结果并没有什么不自然之处,概率法则继续按照它们通常的方式运作。吉尔登斯坦的结果只是隐藏在图的左尾的边缘区域,无限耐心地等待着那些不幸的抛硬币者,他们唯一的错误是遭遇了难以想象的不幸。
参考文献和版权
数据集
从DATA.GOV.IE下载的北东大西洋实时海表面温度数据集,使用CC BY 4.0许可
图片
本文中的所有图片版权归Sachin Date所有,使用CC-BY-NC-SA许可,除非图片下面提到了不同的来源和版权信息。
谢谢阅读!如果您喜欢这篇文章,请关注我,获取关于回归和时间序列分析的技巧、指南和编程建议。