悖论系列 #1
时间和因果关系如何从随机性中产生
两个信封问题会导致悖论和不一致的决策,当使用一个直觉上但错误的贝叶斯概率估计来确定最佳行动方案时出现。纠正数学错误很简单,但问题不止于此:首先,通过微调问题,我们可以使其不可决定——这是语言歧义与数学形式化的对立;其次,当比较几种可能的解决方案时,我们可以观察时间如何在数学世界中出现,从而理论上允许我们测试因果假设。
两个信封问题(TEP)
想象我在桌子上给你展示了两个看似相同的信封,告诉你(不撒谎地)两个信封都装有钱,一个是另一个的两倍,然后我建议你选择其中一个并将里面的钱留给自己。

在你选择一个信封并打开它之前,我问你是否想修改你的选择,选择另一个信封。
你会怎么做?
你可能会告诉我,更换信封是没有意义的,因为无论你选择哪个,情况都是一样的。然而,你应该注意到,你选择了一个未知金额的 x,而另一个信封中的金额 y 可能是 2x 或 x/2,概率相等,这意味着期望金额 y 是 2x (1/2) + x/2 (1/2) = 5x/4,大于 x。所以也许你应该换一个信封?
显然,你也可以根据 y 计算出预期金额 x,因为 x 有一半的机会是 2y 或 y/2,你会发现预期金额 x 是 5y/4,大于 y。
那么这个计算有什么问题?哪个信封更有可能包含更多的钱,如果有的话?
推理中的数学错误
我们可以任意将一个信封标记为“X”,另一个标记为“Y”。现在让我们正确计算当我们知道信封 Y 中的金额为 y 时,信封 X 中金额的条件期望值 E[X|Y = y]。
显然,信封 X 中的金额期望值取决于观察到的具体金额 y:即使在所有可能的 y 值中,信封 X 中的金额可以是 y/2 或 2y,每次的概率都是 1/2,但这并不意味着对于特定的 y 值也是如此。例如,如果 y 是“非常小”(稍后将澄清的意义上),那么 x 大于 y 的机会更大,如果 y 是“非常大”,那么 x 小于 y 的机会更大:在所有可能的 y 值中,概率可以平衡,使得 X 一半的时间是 Y 的一半,一半的时间是 Y 的两倍,但这并不意味着 P(X = y/2|Y = y) = 1/2 和 P(X = 2y|Y = y) = 1/2,只是意味着 P(X = Y/2) = P(X = 2Y) = 1/2。
因此,我们应该尝试正确计算 E[X|Y = y],但首先我们需要澄清导致我们在桌子上有这两个标有“X”和“Y”的信封的过程。让我们假设我们用一个随机金额 U 填充了第一个信封,并用金额 2U 填充了第二个信封。然后我们将它们洗牌,并随机给其中一个信封标记为 X,另一个标记为 Y。我们可以将这个标记过程表示如下:我们抽取一个二进制数字 Z(有一半的机会是 0 或 1)。如果 Z = 0,则 X 是含有金额 U 的信封,否则(如果 Z = 1)是含有金额 2U 的信封。
现在我们可以看到,对于被要求选择但不知道 U 和 Z 被随机选择的外部观察者来说,信封中的金额看起来是这样的:
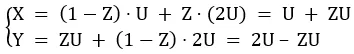
我们可以验证 P(X = 2Y) = P(U + ZU = 4U – 2ZU) = P(3U – 3ZU = 0) = P(U=ZU) = P(Z = 1) = 1/2(对于 P(X = Y/2) 也是一样)。
现在我们可以计算 E[X|Y = y] = E[3U-Y|Y = y] = E[3U|Y = y] – E[Y|Y = y] = 3E[U|Y = y] — y。
我们还需要计算 E[U|Y = y],为此我们需要知道 P(U=u|Y=y),根据贝叶斯定理,P(U=u|Y=y) 与 P(Y=y|U=u)P(U=u) 成正比。
为了计算 P(Y = y|U),我们要知道 Y 是 U 还是 2U,即 U 取值为 y 或 y/2:
- 当 y 不是 u 或 u/2 时,Y = y 的概率为 0:P(Y = y|U = u) = 0
- 当 y 是 u 时,Y = y 的概率为一半(Z = 1):P(Y = y|U = u) = 1/2
- 当 y 是 u/2 时,Y = y 的概率为一半(Z = 0):P(Y = y|U = u) = 1/2
用数学形式表示为:
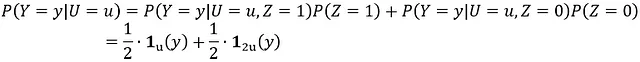
其中:
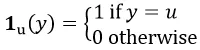
所有这些总结为:
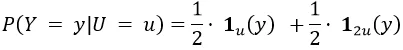
然后我们需要知道 P(U = u),我们只能假设 U 在正实数上是指数分布的(参数 λ>0):
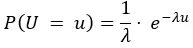
最后,P(U = u|Y = y) 与以下成正比:
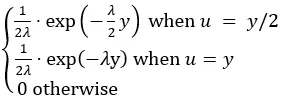
换句话说:
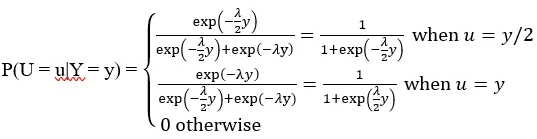
现在我们有了计算 E[X|Y = y] = 3E[U|Y = y] — y 所需的全部信息,即:
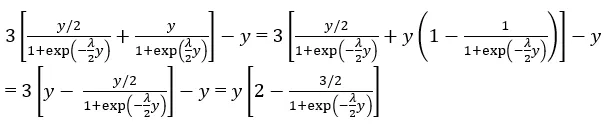
总结一下,我们现在知道:
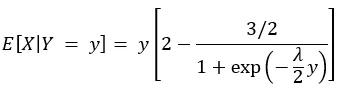
这与最初的 5y/4 很不相同!
当且仅当:
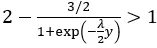
或者换句话说,当且仅当:
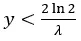
(这是参数λ的指数分布的中位数的两倍,从中获取金额)。
所以我们可以更好地理解我们之前的推理中的错误。虽然按设计,当我们对所有可能的值y进行平均时,X是时间y的两倍,一半时间是这个相同金额的一半,但对于特定的y值,概率不是一半一半的:如果y与从选择值U的方式预期的“大”相比较大,那么信封X包含较小金额的概率更大,如果y“小”,相反,信封X包含较大金额的概率更大。在这里,“大”和“小”的分界线就是指数分布的两倍中位数。
X或Y的选择是对称的,因为E[Y|X = x] = E[3U — X|X = x] = 3E[U|X=x] – x,从而所有以前的计算仍然适用,只是有所改变。
看起来悖论已经解决了,但我声称实际上两个信封问题可能是不可判定的,这意味着我们无法真正知道问题是否对称,或者我们是否应该更喜欢其中一个信封。
一个不可判定的问题
现在假设桌子上放着两个看起来相同的信封,除了它们已经被标记为“X”和“Y”。现在告诉我们信封X中包含Y金额的一半,或者这个金额的两倍,每种可能性都有一半的机会。根据对称性,信封Y也是一样的。现在你被要求选择一个信封:你应该选择哪一个?
根据之前的例子,似乎很明显我们可以随意选择其中一个。然而,这是错误的!这完全取决于我们的假设,或者换句话说,这完全取决于问题的(统计)表达方式。
在这里,当我们被要求选择其中一个时,信封已经被标记的事实是关键。在选择信封中金额的过程和标记它们时是什么样的?如果它们像之前研究的例子中那样是随机标记的,我同意选择其中一个与选择另一个在统计上是等价的。
但是让我们假设X的金额是从正实数上的指数分布中选择的(参数λ>0),类似于之前的例子中对U所做的。然后,信封Y的金额只是随机选择为Y中金额的一半或两倍(具有均匀概率):Y = HX,其中H以1/2或2的值随机选择,每次有一半的机会(H与X独立)。
现在让我们计算Y的累积分布:P(Y < y) = P(HX < y) = P(HX < y |H = 1/2) P(H = 1/2) + P(HX < y |H = 2) P(H = 2)
= P(X/2 < y) (1/2) + P(2X < y) (1/2) = (1/2) P(X < 2y) + (1/2) P(X < y/2)
= (1/2) F(2y) + (1/2) F(y/2) 其中F是X的累积分布函数(指数分布)
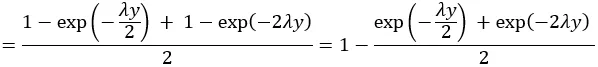
对于非负的y值。
为了得到Y = y的概率密度,我们得到:
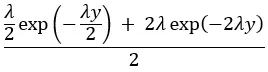
这是指数分布的两个概率密度函数的平均值,一个参数为λ/2,另一个参数为2λ,这意味着信封Y中的平均值是平均值2/λ和1/(2λ)的平均值:
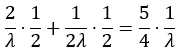
这超过了X的平均值,指数随机变量的参数λ的均值为1/λ(对于那些只关心期望计算的人来说,E[Y] = E[HX] = E[H] E[X],因为H和X是独立的,所以E[Y] = [(1/2)(1/2) + 2(1/2)] E[X] = (5/4)E[X])。
结论是,在这种情况下,如果我们只关心平均值来做决策,那么我们应该系统地选择信封Y。
然而,我们也可以假设不是Y = HX,而是X = HY,其中Y的数量是从参数λ的指数分布中抽取的,那么在这种情况下我们应该选择信封X。
我们对生成桌上两个信封的过程了解不足,无法在没有其他假设的情况下决定应该选择哪个信封。
这就是所有要说的吗?不,最有趣的还在后面。我们可以从我们到目前为止所做的事情中看出,生成信封情况的物理过程必须用随机变量来建模。
但是在物理过程中,有时间:例如,我们选择了一个X的数量,然后我们从中推导出要放入Y的数量,或者反过来;而统计模型能够重新现它,根据X的数量是在Y的数量之前还是之后选择,从而得出不同的结论。换句话说,我们的统计模型能够在数学上重新现实际中的时间。
时间和因果关系从随机性中的出现
经常有人说数学只能证明相关性,而不能证明因果关系。在这方面,计量经济学中的因果分析只是与数学相关的相关性分析。是人类决定一个事件是另一个事件的结果,基于两个事件之间的相关性和时间:在第一个事件之后发生的事件只能是结果,而不是原因。
因为时间不是一个数学概念,而是一个物理概念,数学似乎无法独立于任何关于哪个现象首先发生(因此被称为原因)和哪个现象其次发生(因此被称为结果)的人类输入来建立因果关系。但是真的是这样吗?时间的概念源于不可逆性的概念:当一个物体从左到右移动时,这不是因为时间而产生的变化,因为物体可以返回到其原始位置;当一个物体变老时,这是由于时间流逝而发生的变化,因为这个过程是不可逆的。时间是世界状态的不可逆变化。
在物理学中,不可逆性被视为无序增加的结果,形式上称为熵:正因为组成物体的分子变得更加无序,物体将永远无法恢复到其初始状态,因此变化不仅被视为发生在时间上,而且因为时间而发生。虽然状态的变化足以说明时间的流逝,但物理上的不可逆性使得时间只能以一个方向流动,使我们能够区分原因和结果。
在不深入细节的情况下,只有一个老化物体的宏观状态是不可逆的:从理论物理学的观点来看,从微观层面上,分子和粒子可以以类似于过去状态的方式重新排列。因此,物理上的不可逆性不能简单地由一个不可逆的数学函数来建模,因为这个特性将不存在。相反,随机变量在宏观上是不可逆的,但在微观上是可逆的:例如,如果Y = HX,这并不意味着X = Y/H(从宏观的角度来看是不可逆的),但对于Y、H和X取任意值y、h和x,y = hx和x = y/h(从微观的角度来看是可逆的)。这个两个信封的悖论特别令人困惑,因为在其表述中一切似乎是对称的(如果x是y的一半或两倍,那么意味着y是x的两倍或一半),然而这只在“微观”水平上成立。
但是物理熵和随机变量之间的联系如何有助于研究因果关系呢?
让我们再次考虑最后一个例子,两个预先标记的信封X和Y,假设我们知道要么Y = HX,要么X = HY,意味着要么Y是X的结果,要么反过来。我们可以通过观察X和Y的大量观察来测试每个假设,以便确定这两个随机变量的概率密度,并且其中一个将具有更”熵”的密度(在一些特定的要测试的数学关系下更”熵”),因为它将基于另一个随机变量的密度,但由随机变量H(其密度被假定已知)”打乱”。
现在让我们考虑更常见的问题。通常使用线性回归来量化多个变量之间的因果关系。例如,假设Y = αX,我们假设Y是X的结果,并且我们想量化因果系数α。然而,这并不能以任何方式证明从X到Y的因果关系,它只能在假设为真的情况下量化X和Y之间的假设关系。
对于这样一个简单的例子,假设Y等于αX,无法在数学上确定因果关系,因为这等价于说X = Y/α。然而,如果系数α被认为是更一般过程A的一个历史值,那么就可以比较Y、A和X的分布,看哪一个更符合Y = AX或X = Y/A的假设。另一个例子是研究关系Z = X + Y(Z由X和Y引起),与其他可能性进行比较,例如Y = Z – X(Y由X和Z引起):比较X、Y和Z的分布能够解决因果问题。
虽然这些考虑在实际生活中并不直接有用,因为准确估计随机变量的分布可能是昂贵、复杂或不可行的,但可以想象使用聚合来进行因果分析。例如,在Y = HX和X = HY之间选择时,我们已经看到在第一种情况下E[Y] > E[X],在第二种情况下E[X] > E[Y]。在线性关系的情况下,我们可能需要测试X = Y + Z、Y = X – Z和Z = X – Y之间的关系,但期望值不是有用的(除非我们取指数,例如exp(X)=exp(Y)exp(Z)),因为在每种情况下E[X]都等于E[Y] + E[Z],但关系Var(X) = Var(Y) + Var(Z) + 2Cov(Y, Z)只在第一种情况下成立。
这些技术可以提供有关因果关系的有用指示,并有助于测试假设。但更重要的是,我们的物理世界的物理时间如何从随机性的概念中在数学世界中出现,这难道不是美丽的吗?
结论
从分析一个众所周知的统计学“悖论”——两个信封问题开始,我们认识到这个悖论的出现不仅是因为问题的天真解法存在数学上的缺陷,而且由于人类语言中的一些模糊性,使得两个不同的随机变量函数(HX和X/H)看起来是等价的。
进一步挖掘发现,涉及随机变量的方程,在一般情况下无法“逆转”(宏观视图),但在考虑随机变量的实现(微观视图)时是“可逆转”的。
因此,我们提出了随机变量的样本空间Ω与物理系统的相空间之间的类比,随后观察到了统计世界中“物理熵”的出现,从而引发了不可逆性和时间的出现。
最后,在我们的晦涩计算中时间出现后,我们能够对超越简单相关分析的因果假设测试方法得出结论。所有这些都源于两个信封!