学习为什么线性回归是这样的,以及如何通过各种方式自然地扩展它
大多数有志于成为数据科学博主的人都会写一篇关于线性回归的介绍文章——这是进入这个领域时我们学习的第一个模型,所以这是一个自然的选择。虽然这些文章对初学者来说很好,但大多数都不够深入,无法满足高级数据科学家的需求。
因此,让我带你走进一些不为人知但又耳目一新的线性回归细节,这将使你成为一个更好的数据科学家(并在面试中获得加分)。
这篇文章相当数学密集,因此为了跟上,有一定的概率和微积分基础会很有益。
数据生成过程
当建模时,我非常喜欢思考数据生成过程。处理贝叶斯建模的人知道我在说什么,但对于其他人来说:想象一下你有一个数据集(X,y),由样本(x,y)组成。给定x,如何到达目标y?
让我们假设我们有n个数据点,每个x有k个组件/特征。
对于具有参数w₁,…,wₖ(系数),b(截距),σ(噪声)的线性模型,假设数据生成过程如下:
- 计算µ = w₁x₁ + w₂x₂ + … + wₖxₖ + b。
- 滚动一个随机的y〜N(µ,σ²)。这与其他随机生成的数字无关。或者:滚动ε〜N(0,σ²),并输出y = µ + ε。
就这样了。这两行简单的代码等同于人们喜欢解释的最重要的线性回归假设,即线性、同方差性和误差独立性。
从过程的第一步中,您还可以看到我们使用典型的线性方程w₁x₁ + w₂x₂ + … + wₖxₖ + b来模拟期望µ,而不是真实的目标。我们知道我们不会击中目标,所以我们会满足于生成y的分布的平均值。
扩展
广义线性模型。我们不必强制使用正态分布来进行生成过程。如果我们处理的数据集只包含正目标,则假设使用泊松分布 Poi(µ)而不是正态分布可能会更有益。这就为您提供了泊松回归。
如果我们的数据集仅具有目标0和1,则使用伯努利分布 Ber(p),其中p = sigmoid(µ),那么您就得到了逻辑回归。
只有0、1、…、n之间的数字?使用二项分布来获得二项回归。
列表还可以继续。长话短说:
考虑一下哪种分布可能生成了您在数据中观察到的标签。
我们实际上在最小化什么?
好的,所以我们现在决定了一个模型。现在我们如何训练它?我们如何学习参数?当然,你知道:我们最小化(平均)平方误差。但为什么?
秘密在于,您只需使用我们先前描述的生成过程进行计划最大似然估计。我们观察到的标签是y₁、y₂、…、yₙ,所有这些标签都通过具有平均值µ₁、µ₂、…、µₙ的正态分布独立生成。看到这些y的可能性是多少?它是:
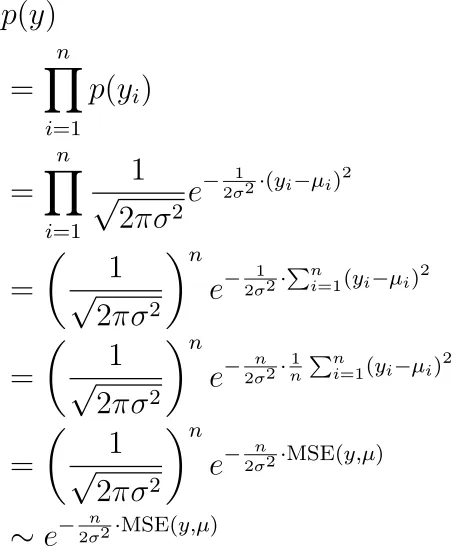
现在我们想要寻找(隐藏在 µᵢ 中的)参数,以最大化这个项。正如您所看到的那样,这等同于最小化均方误差。
扩展
不等的方差。实际上,σ不必保持恒定。您的数据集中每个观测值可以有不同的σᵢ。然后,您将最小化
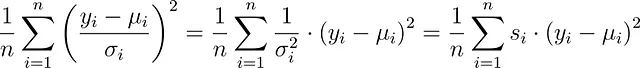
这是带有样本权重s的最小二乘法。建模库通常允许您设置这些权重。例如,在scikit-learn中,您可以在fit函数中设置sample_weight关键字。
这样,您可以通过增加相应的s来更加强调某些观测值。这等同于减小方差σ²,也就是说,您更加确信这个观测值的误差更小。这种方法也称为加权最小二乘法。
与输入有关的方差。您甚至可以说方差也取决于输入x。在这种情况下,您将得到有趣的损失函数,也称为方差衰减:

整个推导过程概述如下:
免费为回归神经网络获得不确定性估计
给定正确的损失函数,标准神经网络也可以输出不确定性
towardsdatascience.com
正则化。您可以采取贝叶斯观点,并最大化后验概率似然,而不仅仅是最大化观察标签y₁,y₂,…,yₙ的可能性。
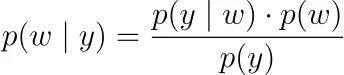
在这里,p(y|w)是上面的可能性函数。我们必须为p(w)选择一个概率密度,即所谓的先验分布。如果我们说参数独立地以0为中心的正态分布,即wᵢ ~ N(0, ν²),那么我们最终得到L2正则化,即岭回归。对于拉普拉斯分布,我们得到L1正则化,即LASSO。
为什么会这样?让我们以正态分布为例。我们有
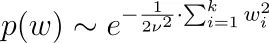
因此,与我们从上面的p(y|w)公式一起,我们必须最大化
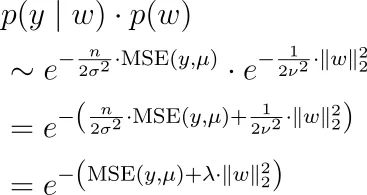
这意味着我们必须最小化均方误差加上一些正则化超参数时间w的L2范数。
请注意,我们从贝叶斯公式中省略了分母 p(y),因为它不取决于 w,因此我们可以在优化时忽略它。
您可以使用任何其他先验分布来创建更有趣的正则化。您甚至可以说您的参数 w 符合正态分布,但与某些相关矩阵 Σ 相关。
假设 Σ 是正定的,即我们处于非退化的情况。否则,没有密度 p(w)。
如果您进行数学计算,您将发现我们需要优化
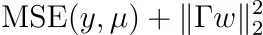
针对某些矩阵 Γ。 注意:Γ是可逆的,我们有 Σ⁻¹ = ΓᵀΓ。 这也被称为 Tikhonov 正则化。
提示:从以下事实开始
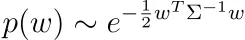
并记住正定矩阵可以分解为某些可逆矩阵及其转置的乘积。
最小化损失函数
很好,我们定义了我们的模型并知道要优化什么。但是,我们如何进行优化,即学习最小化损失函数的最佳参数?什么时候有唯一的解?让我们来看看。
普通最小二乘
假设我们不进行正则化,也不使用样本权重。然后,均方误差可以写成
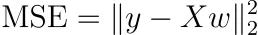
这相当抽象,所以让我们写成另一种形式
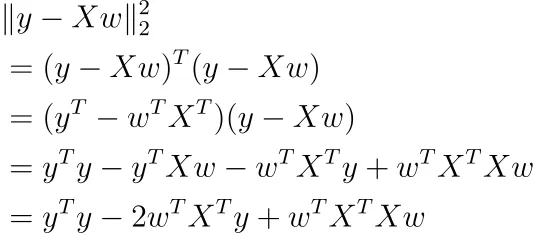
使用矩阵微积分,您可以对此函数关于 w 取导数(我们假设偏置项 b 已包含在内)。
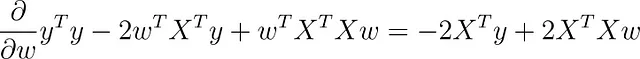
如果您将此梯度设置为零,您将得到
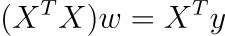
如果 ( n × k )-矩阵 X 的秩为 k,则 ( k × k )-矩阵 X ᵀ X 的秩也为 k,即它是可逆的。为什么?它遵循 rank(X) = rank(X ᵀ X)。
在这种情况下,我们得到 唯一的解
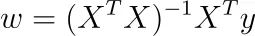
注意:软件包不会像这样进行优化,而是使用梯度下降或其他迭代技术,因为它更快。尽管如此,这个公式很好,可以为我们提供一些关于问题的高层次见解。
但这真的是最小值吗?我们可以通过计算 Hessian (即 X ᵀ X) 来找出答案。这个矩阵是半正定的,因为对于任何 w ,w ᵀ X ᵀ Xw = |Xw|² ≥ 0。它甚至是严格正定的,因为 X ᵀ X 是可逆的,即 0 不是其特征向量,所以我们的最优 w 确实是在最小化我们的问题。
完美的多重共线性
这是友好的情况。但是如果 X 的秩小于 k 会发生什么?如果我们的数据集中有两个特征,其中一个是另一个的倍数,例如我们在数据集中使用身高(以米为单位)和身高(以厘米为单位)这两个特征,那么我们就有身高(以厘米为单位)= 100 * 身高(以米为单位)。
如果我们对分类数据进行独热编码并且没有删除其中一列,也会出现这种情况。例如,如果我们的数据集中有颜色这个特征,可以是红色、绿色或蓝色,那么我们可以进行独热编码,得到三列 color_red、color_green 和 color_blue。对于这些特征,我们有 color_red + color_green + color_blue = 1,这也会导致完美的多重共线性。
在这些情况下,X ᵀ X 的秩也小于 k,因此这个矩阵不可逆。
故事结束。
还是没有?实际上不是,因为这可能意味着两件事:( X ᵀ X ) w = X ᵀ y 无解或有无限多个解。
事实证明,在我们的情况下,我们可以使用 Moore-Penrose 逆来获得一个解。这意味着我们处于有无限多个解的情况,所有这些解都给出了相同的(训练)均方误差损失。
如果我们用 A ⁺ 表示 A 的 Moore-Penrose 逆,我们可以解线性方程组
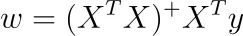
要获得其他无限多个解,只需将 X ᵀ X 的零空间添加到此特定解中。
Tikhonov 正则化下的最小化
回想一下,我们可以将先验分布添加到我们的权重中。然后我们必须最小化
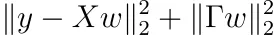
对于某些可逆矩阵 Γ。按照普通最小二乘法的步骤,即对 w 求导并将结果设为零,我们得到的解为
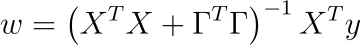
好的部分是:
XᵀX + ΓᵀΓ 总是可逆的!
让我们找出为什么。只需证明 X ᵀ X + ΓᵀΓ 的零空间只有 {0} 即可。因此,让我们取一个 w,使得 ( X ᵀ X + ΓᵀΓ) w = 0。现在,我们的目标是证明 w = 0。
从 ( X ᵀ X + ΓᵀΓ) w = 0,我们得到:
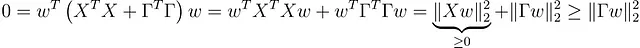
这又意味着 |Γ w | = 0 → Γ w = 0。由于 Γ 是可逆的,因此 w 必须为 0。使用相同的计算,我们可以看到 Hessian 也是正定的。
很好,Tikhonov正则化自动帮助使解唯一!由于岭回归是Tikhonov回归的一个特例(对于Γ = λ Iₖ,Iₖ是k维单位矩阵),同样适用于岭回归。
添加样本权重
最后,让我们还将样本权重添加到Tikhonov正则化中。添加样本权重等价于最小化
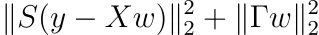
对于某些具有正对角线条目sᵢ的对角矩阵S。最小化与普通最小二乘法一样简单。结果为
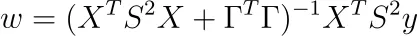
注意:海森矩阵也是正定的。
给你的作业
假设对于Tikhonov正则化,我们不要求权重围绕0为中心,而是某个其他点w₀。证明优化问题变为
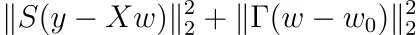
并且解为
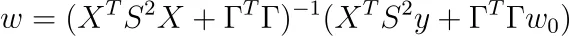
这是Tikhov正则化的最一般形式。有些人更喜欢像这样定义P:= S²,Q:= ΓᵀΓ。
结论
在本文中,我带您走过了线性回归的几个高级方面。通过采用生成视图,我们可以看到广义线性模型与普通线性模型之间仅在用于采样目标y的分布类型上有所不同。
然后,我们发现最小化均方误差等价于最大化观察值的似然。如果在可学习参数上施加先验正态分布,我们最终得到Tikhonov(和L2作为特例)正则化。我们也可以使用不同的先验分布,例如拉普拉斯分布,但是那样就没有闭合解公式了。尽管如此,凸规划方法也可以让您找到最佳参数。
作为最后一步,我们为每个最小化问题找到了许多直接解决方案公式。对于大型数据集,这些公式通常不用于实践,但我们可以看到解决方案始终是唯一的。我们还学会了一些微积分。😉
我希望您今天学到了新的、有趣的、有价值的东西。谢谢阅读!
最后,如果您
- 想要支持我写更多关于机器学习的文章,并且
- 计划购买小猪AI订阅,
为什么不通过这个链接来购买呢?这会对我有很大的帮助!😊
为了透明,您的价格不会改变,但约一半的订阅费用将直接支付给我。
如果您考虑支持我,非常感谢!
如果您有任何问题,请在LinkedIn上与我联系!