梯度下降法的技术描述,结合算法工作的图形表示

- 引言:一些关键定义
在优化方法中,尤其是一阶算法类型中,大家一定听说过梯度下降法。它属于一阶优化类型,因为它需要一阶导数,即梯度。通过优化,梯度下降法旨在最小化“实际”输出与模型预测输出之间的差异,这由目标函数衡量,即成本函数。梯度,或者斜率,定义为在给定的函数(曲线或直线)上的某一点处绘制的线的方向。迭代地,梯度下降法旨在区分成本函数在线的不同点处的导数,从而得出这些点的方向变化程度,并朝最陡的下降方向迈进,即局部最小值。正如其名称所示,梯度被用作朝最陡的下降方向搜索局部最小值的方向,其中被优化的成本函数的参数值被最小化,即取得最低值。
梯度下降法主要用于(等等)训练机器学习模型和深度学习模型,后者基于神经网络架构类型。从线性回归和逻辑回归到神经网络,梯度下降法旨在计算函数的最佳参数值。在其最简单的形式中,梯度下降法旨在通过推导出独立变量的最优参数值来最小化下面线性回归的误差项。即:
y = β0 + β1 * X1 + … βk * Xk + Ɛ
其中,
y是因变量
k是独立变量的数量
X是独立变量
β是参数
Ɛ是误差项组成部分
在其更复杂的形式中,梯度下降法在编译阶段时通常被定义为训练深度学习模型的优化器。深度学习基于一个相互连接的网络来不断学习和改进,即神经网络。受到人脑的启发,神经网络是由人工神经元(称为节点)表示的高度复杂的网络。在顶层,节点的重要角色是处理和分析来自前一层节点的数据,并将其传递给下一层节点。在神经网络中,权重,即用于优化的参数,是节点之间的连接。它们是输入/特征与隐藏层之间的联系,因此它们代表了预测最终输出时给定特征的重要性。找到单个权重的最优值取决于许多权重的值。而这种优化是同时针对许多权重进行的,在深度神经网络中,即使在数百万的规模中也可能非常大。在这里,梯度下降法在涉及大量计算的情况下表现出极高的效率,这些计算基于神经网络的三个主要层:1)输入层2)隐藏层和3)输出层。
有许多论文适当详细地阐述了深度学习和估计函数参数值的方法,因此展开了梯度下降法和普通最小二乘法(OLS)之间的差异,例如在线性回归的情况下。由于这不是本文的重点,读者被促请进一步研究和扩展,以更好地理解这些方法。
2. 是时候进行一些微积分了!
为了更好地理解梯度下降法,我们需要对可微函数的定义进行扩展。当导数可以在该函数所得到的曲线的任意一点上定义时,一个函数,明确地说是ƒ(x),就是可微的。换句话说,在函数ƒ(x)的定义域中的所有点上。在这里,有两个概念加强了这个定义:一阶导数和二阶导数。一阶导数的公式定义如下:
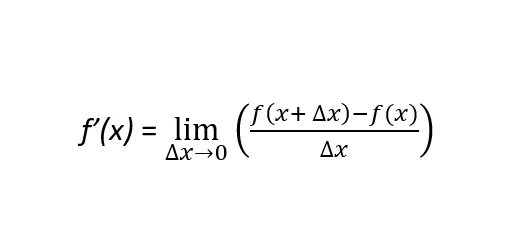
严格来说,一个函数的一阶导数,记作ƒ’(x)或df(x)/dx,是函数ƒ(x)在给定点x的斜率。如果斜率为正(负),则表示函数增加(减少)的程度。正斜率表示随着x的值增加,函数ƒ(x)也增加。相反,负斜率表示随着x的值增加,ƒ(x)减少。二阶导数是函数ƒ(x)的导数的导数。记作ƒ’’(x)或d2f(x)/dx2,二阶导数表示函数ƒ(x)的形状。也就是说,函数是凹的还是凸的。从数学角度来说,(这一点非常重要!!!)二阶导数可以区分相对最大值和相对最小值。
其中,
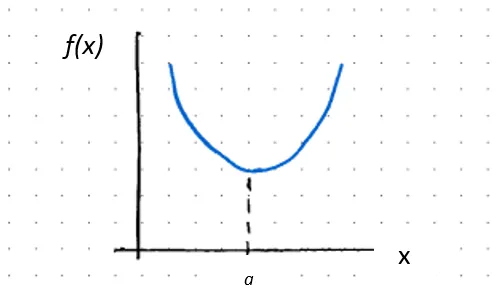
ƒ’’(x) > 0,那么ƒ(x)在x = a处是凸的
如果ƒ’(a) = 0,则a是临界点,因此是相对最小值
其中,
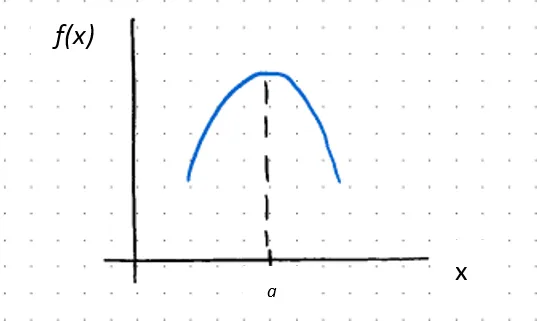
ƒ’’(x) < 0,那么ƒ(x)在x = a处是凹的
如果ƒ’(a) = 0,则a是临界点,因此是相对最大值
或者如果二阶导数等于零,那么要么1)函数ƒ(x)处于拐点,称为拐点,从凹变为凸或从凸变为凹,要么2)该点上的函数未定义(即不连续)。在前一种情况下:
ƒ’’(x) = 0,则ƒ(x)在x = 2处是一个拐点

上述内容主要关注单变量函数,即只有一个自变量的函数,y = ƒ(x)。在现实世界中,人们将研究和建模多变量函数,其中所研究的变量受到多个因素的影响,即两个或更多个自变量,y = ƒ(x, z)。为了衡量自变量x的变化对因变量y的影响,保持z不变,需要对函数进行偏导数的计算。因此,偏导数计算了由于每个输入的变化而引起的成本函数的变化率。梯度下降算法迭代地计算这些成本函数的变化,并在每个不同的步骤更新这些函数的参数值,直到达到最小点,其中参数的值被优化,因此成本函数被最小化。
3. 梯度下降算法的工作原理
斜率的绝对值越大,我们可以走得越远,和/或我们可以不断地朝着最陡的下降方向前进,即局部最小值。当我们接近最低点/最小值时,斜率减小,所以我们可以采取更小的步骤,直到达到斜率等于零的平坦表面(ƒ’(x) = 0),这是图表中红色箭头指向的βi的最低值。这是曲线线的局部最小值,也是函数参数的最佳值。

因此,如果一个函数是严格凸(凹)的,那么只会有一个临界点。现在,还存在一种情况,即存在多个局部最小值。在这种情况下,搜索的目标是函数能够达到的最低值。这被称为全局最小值。

以下两个关键问题出现:
1) 要朝哪个方向迈出步伐?
2) 步伐应该有多大?
让我们回顾一下目前为止我们所说的内容。梯度下降是一种算法,在模型的训练阶段中,通过在每一步中获取函数相对于每个输入的偏导数,以朝着最陡的下降方向即局部最小值迭代调整和优化函数参数的值。如果导数为正数,函数是递增的。因此,应该朝相反的方向迈出步伐。梯度指示应该朝哪个方向迈出步伐。如果梯度很大,即斜率绝对值很大,应该朝局部最小值迈出较大的步伐。事实上,梯度下降在每次迭代中朝向局部最小值的方向上采取越来越小的步伐,如上图中的蓝色箭头所示。
步伐大小与学习率有关。这是算法学习/朝最陡下降方向移动的速度。在梯度最大的情况下,即斜率的绝对值最大,算法学习得最快。随着接近局部最小值,采取的步伐越小。因此,学习率作为超参数是在尝试不同的值后设置的,以便在迭代过程中降低成本函数。如果太大,可能会错过局部最小值。学习率过小可能导致权重的更新不显著改进模型。如果太小,将需要较长时间才能达到收敛。当成本函数不再减小时,达到收敛。因此,成本函数是算法性能的指标。在多元函数世界中,这表示:
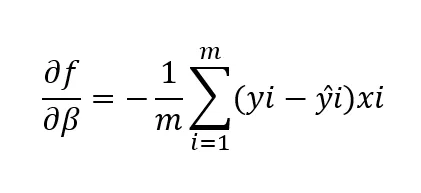
其中,
df/dβ是成本函数关于参数β的偏导数
m是数据点的数量
yi是第i个数据点的实际依赖/目标变量的值
ŷi是模型对第i个数据点的依赖/目标变量的预测值
xi代表与数据点相关联的第i个输入。
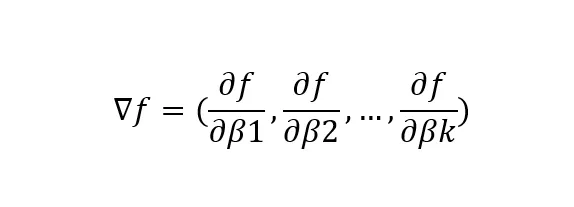
其中,
▽f代表函数f(x)关于参数β的梯度向量
df/dβk代表函数f(x)关于第k个参数β的偏导数
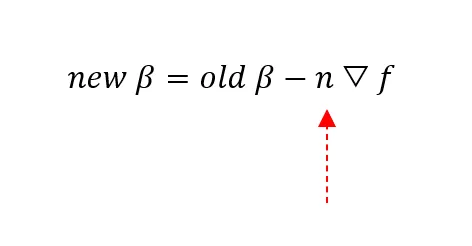
其中,
New β代表第i个参数β的当前值
Old β代表第i个参数β的更新值
n是学习率:要采取的步伐的长度!
▽f是指向最陡下降方向的函数f(x)相对于参数β的梯度向量,以最小化f(x)
4. 梯度下降的局限性
梯度下降的局限性之一与前面提到的一个标准有关,即函数在其定义域的每一点上都必须可微。当不满足这个条件时,算法找到一个未定义的点(即非连续点)时,它将失败。
另一个局限性与朝最陡下降方向采取的步伐大小,即学习率(n)有关。如果步伐太大,很可能会错过局部最小值,甚至无法达到收敛。如果步伐太小,收敛所需的时间将更长。如果输入的数量很大,这个问题变得更加棘手。
最后,梯度下降可能永远无法找到全局最小值。该算法无法区分局部最小值和全局最小值。当它下降寻找局部最小值时,一旦收敛,它就会停止。局部最小值将把算法困在自己的山谷中,使步长不足以足够大以退出。
5. 结论
总之,梯度下降是:
1)迭代的一阶优化算法类型
2)在每次迭代中,可微分函数的参数被更新,从而使代价函数最小化。
3)因此,收敛是在局部最小值上实现的。
基于梯度下降的局限性,有动机去探索不同和更高级的梯度下降方法,甚至是在优化领域中的其他类型的算法,如二阶类型。然而,这超出了本文的范围,因此我将把它作为下一篇文章的主题 😊
感谢阅读!
请添加任何您认为可以增加该主题知识的评论!