一切关于狄利克雷分布的知识
狄利克雷分布是贝叶斯统计学中贝塔分布的一般化。在贝叶斯统计学中,它常被用作多项式分布的共轭先验,因此可以用来模拟随机概率向量的不确定性。它在贝叶斯分析、文本挖掘、统计遗传学和非参数推断等领域有广泛的应用。本文直观地介绍了狄利克雷分布,并展示了它与多项式分布的联系。此外,还展示了如何在Python中对其进行建模和可视化。
定义
假设连续随机变量X₁,X₂,…Xₖ(k≥2)构成了定义为X的随机向量:
我们还定义了向量α如下:
其中
现在,如果随机向量X具有参数为α的狄利克雷分布,则它具有以下联合概率密度函数:
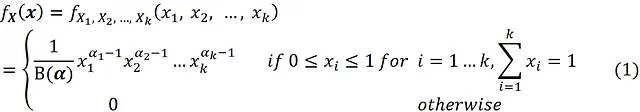
函数B(α)称为多元贝塔函数,定义为
其中Γ(x)是伽玛函数。如果随机向量X具有参数为α的狄利克雷分布,表示为X ~ Dir(α)。多元贝塔函数被包含在联合概率密度函数中以使其归一化。联合概率密度函数在其定义域上应该积分为1:
因此,我们有:
根据方程1,随机变量X₁,X₂,…Xₖ所取的值应满足以下条件以满足fₓ(x)>0:
这些条件定义了狄利克雷分布的支撑集。支撑集是X和其分布的一组所有x(X可以取的值)的集合,其中fₓ(x)>0。如果X有k个元素,则具有狄利克雷分布的X的支撑集是一个k-1维的单纯形。单纯形是由方程3的约束条件创建的有界线性流形。单纯形是将三角形的概念推广到更高维度的一般化。因此,k-1维单纯形是…