
在这里,我们获取了魔方最优解的概率
魔方是一个具有巨大状态空间和唯一解的规划问题的原型。它是干草堆中的针的定义。如果没有任何指导(即使你可以每秒转动一百次),你可能会花费整个宇宙的时间也无法成功。关于它的一切似乎都涉及到巨大的数字。
我们要计算的数量是一个例外。通过它,您将对一个困难的问题(以及任何类似的规划问题)有一个简单的视角。我们需要两个要素,一个随机过程和一个最优解器。最后一个是一种能够使用最少的移动次数解决魔方(或类似问题)的设备(真实或理想),给定任何初始状态。我们将完全回答以下问题:
如果一个已解决的魔方经历了N次随机转动,一个最优解器需要确切地d次移动才能将其解决的概率p(d|N)是多少?
在正常情况下,如果有人让你解决魔方,你只会得到一个没有参考或标签的打乱魔方。在这里,我们有关于乱序状态的一条信息:它是在已解决状态下通过N次随机移动得到的。这个信息是有用的!
我们为什么对p(d|N)感兴趣?
在计算上,您可以以不同的方式解密魔方。魔方项目的野心可以在解决任何或某些状态的非最优解和最优解之间变化(例如,这将需要35个著名的CPU年)。魔方求解器通常涉及两个方面,搜索算法和启发式函数。通过选择这两个参数,我们可以确定我们的方法的难度、效率或计算要求。
在启发式函数领域,即搜索指导方面,总是有新思路的空间。从历史上看,魔方的启发式函数是使用曼哈顿距离估计来确定乱序魔方方格相对于其解决位置的组合。直到最近才使用神经网络作为启发式函数。
神经网络=魔方新启发式函数
神经网络的工作很简单(分类器):您提供魔方状态x,并预测该状态的深度d。状态的深度d定义为解决魔方所需的最小移动次数。注意以下内容。如果我们有一个能够知道任何状态的深度的设备,我们实际上就有了一个最优解器,因为每次我们可以选择给我们提供具有较低深度的状态的移动,直到我们达到深度=0(已解决状态)。
问题在于如何训练该网络。或者,具体地说,如何获取准确的训练数据。除非您已经有了一个最优解器,否则很难知道乱序状态x的实际深度。我们没有一个最优解器,或者我们不想使用计算昂贵的解器。我们想从零开始构建一个近似和高效的最优解器,并为其提供准确的训练数据:
training_data = (x,d)。
正如我们所说,准确度d很难获得,但是可以将一个数字N与某些特定的乱序状态相关联:即通过对已解决的状态进行N次随机移动产生的状态。然后
p(d|N)估计给定N的d。
p(d|N)将用于提高训练数据的准确性。以上述论文的作者为例,他们构建了第一个魔方深度分类器神经网络。他们的训练数据的形式为:
训练数据 = (x , N).
他们将 d 作为 N。这个选择通过在训练期间使用类似Bellman的循环动态提高标签的准确性来补偿。在这里计算的概率 p(d|N) 为训练数据的准确性提供了一个更好的起点(仅通过随机扭曲已解决的状态 N 多次获得)。
随机行走视图
计算 p(d|N) 相当于问一个随机行走者在经过 N 步后距离 d 有多远。他不是在一个方格网络中行走,而是在一个拥有10的19次方个节点(魔方的状态)和相似数量的连接(合法移动)的巨大魔方图中行走。如果我们选择一个节点按照它们的深度组织的布局:解决状态在中心,深度为 d 的状态位于距离中心 d 的半径上,那么图形将看起来非常对称。径向(深度)方向提供了一个非常简单的视角。
约定
在3x3x3魔方中,我们采用所谓的四分之一转动度量,其中一个移动涉及90度的面转动,可以顺时针或逆时针。在这个度量中,有12种可能的移动。如果我们选择了不同的度量,比如半转动度量(也包括180度面转动作为单个移动),那么 p(d|N) 的表达式将不同。
数据
为了获得 p(d|N) ,我们需要使用某种领域知识,但我们不想涉及图形、模式数据库或群论。我们将使用一些更“原始”的东西:
包含深度为 d 的魔方状态的种群列表。
这个列表(由2012年“上帝之数”论文的作者提供)没有指定哪些状态处于某个深度,只有它们的总数,并且没有涉及任何 N。
# 深度种群列表# 在四分之一转动度量中深度为d的魔方状态的数量 D_d={# 深度 状态数量 0: 1, 1: 12, 2: 114, 3: 1068, 4: 10011, 5: 93840, 6: 878880, 7: 8221632, 8: 76843595, 9: 717789576, 10: 6701836858, 11: 62549615248, 12: 583570100997, 13: 5442351625028, 14: 50729620202582, 15: 472495678811004, 16: 4393570406220123, 17: 40648181519827392, 18: 368071526203620348, 19: 3000000000000000000, # 近似值 20: 14000000000000000000, # 近似值 21: 19000000000000000000, # 近似值 22: 7000000000000000000, # 近似值 23: 24000000000000000, # 近似值 24: 150000, # 近似值 25: 36, 26: 3, 27: 0}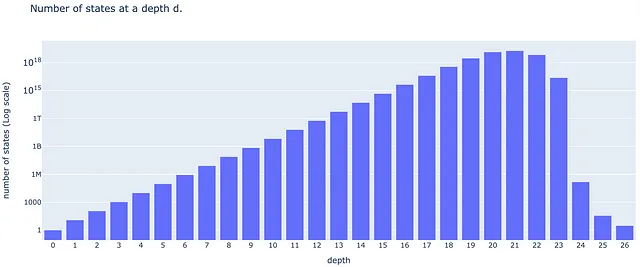
关于这个列表的一些观察:
首先,深度大于26的状态数为零(四分之一转动度量的上帝之数是26)。其次,该列表报告了 d 在19到24之间的状态的近似数量。我们以后需要小心处理这一点。第三,如果我们制作一个对数尺度的图形,我们可以看到大多数深度(除了接近末尾的深度)呈线性增长。这意味着状态种群 D(d) 呈指数增长。通过用一条直线拟合对数图的线性部分,我们可以了解到在 d = 3 和 d = 18 之间状态种群的增长方式为
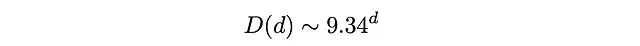
在深度3 < d < 18的情况下,平均而言,12个移动中有9.34个会使你离开已解决的状态,而2.66个会使你接近。
深度类别上的马尔可夫过程
为了找到p(d|N),我们将深度类别想象成马尔可夫过程中的站点。让我解释一下:

深度类别d是在深度d(到达已解决状态所需的最小移动次数)下的所有魔方状态的集合。如果我们在深度类别d中随机选择一个状态,并用一个随机移动随机转动一个面,那么我们会以概率p_d得到一个在类别d + 1中的状态,或者以概率q_d得到一个在类别d – 1中的状态。在切换度量中,没有自身类别的移动。
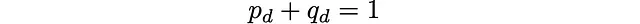
这定义了一个马尔可夫过程,其中特定的站点是一个完整的深度类别。在我们的情况下,只有相邻的d类别之间才有一次跳跃的连接。准确地说,这是一个离散时间的出生-死亡马尔可夫链。由于站点数量是有限的,该链也是不可约和遍历的,并且存在唯一的平稳分布。
我们假设在每次选择随机移动时,概率是均匀分布的。这会导致一些在深度类别之间的过渡概率p_d, q_d(需要计算)。随机移动的次数N是马尔可夫过程的离散时间。这也是一个一维随机行走器:在每个站点(深度类别编号d),向前走的概率是p_d,向后走的概率是q_d。这个一维链条,粗略地说,是魔方图中的“径向”方向(以深度-径向布局组织)。
过渡矩阵
任何马尔可夫过程都可以用过渡矩阵M来编码。矩阵M的(i,j)条目是从站点i跳转到站点j的概率。在我们的情况下,只有以下条目与零不同:


这里p_0 = 1:从深度类别0(仅包含已解决的状态)只能跳到深度类别1(没有类别-1)。同样,q_26 = 1:从深度类别26只能跳到深度类别25(没有类别27)。出于同样的原因,没有p_26或q_0。
平稳分布
我们将随机移动立方体的动作映射为一维深度类随机行走者在概率q_d和p_d之间来回跳跃。经过长时间行走后会发生什么?或者说长时间行走后行走者访问特定位置的次数有多少?在现实生活中,当立方体进行随机转动时,深度类被访问的频率是多少?
从长期来看,无论起点是什么,行走者在深度类d中停留的时间与该深度类的人口D(d)成比例。这是重点:
(标准化的)深度人口列表D(d)应被解释为代表我们的深度类马尔可夫过程的稳态分布的向量。
数学上,D(d)是M的左特征向量
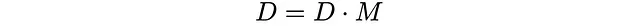
这个矩阵方程将给我们26个线性方程,从中我们将得到p_i’和q_i。
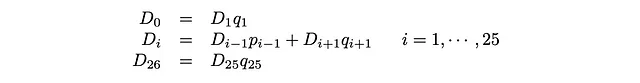
考虑到p_0 = q_26 = 1,我们可以将其重新写成

这些被称为详细平衡方程:定义为稳态站点人口乘以跳跃概率的通量在两个方向上是相同的。解是:
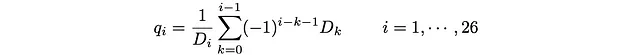
和p_i通过p_i + q_i = 1获得。
深度类人口的一些条件
这些解有趣的地方在于,因为q_i是一个概率,我们应该有
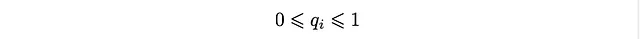
这导致了分布D_k的以下条件:
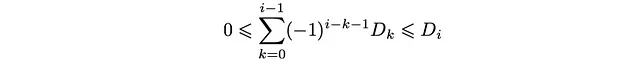
这是深度人口D_k应满足的一系列不等式。明确地说,它们可以组织为:
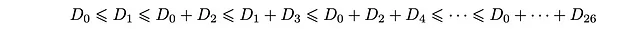
特别地,最后两个不等式是
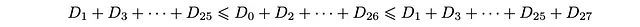
因为D_27 = 0,所以下界和上界相等,因此
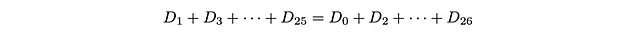
或者:
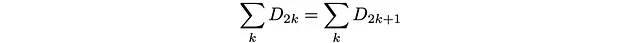
偶数位点的人口之和应等于奇数位点的人口之和!
我们可以将其视为偶数和奇数位置之间的详细平衡:每次移动都是到一个不同且相邻的深度类别。任何跳跃都会将您从奇数深度类别(所有奇数深度类别的类别)跳到偶数深度类别(所有偶数深度类别的类别)。因此,奇数到偶数类别的跳跃的概率为1(反之亦然)。由于两个方向的概率都为1,根据详细平衡原理,它们的数量应该相等。
出于同样的原因,马尔可夫过程在每次移动后将达到一个周期为二的“稳态分布”,在偶数和奇数位置之间切换(离散时间 N)。
数据的问题
我们计划使用的数据源中报告的深度-人口D_d对于d = 19、20、21、22、23、24是近似值。因此,不能保证它将满足所有这些条件(不等式)。如果我们得到一些不在范围[0,1]内的概率q_i(正是这种情况!),请不要感到惊讶。特别是,如果我们尝试检查最后一个条件(偶数-奇数人口相等),结果会差很多!(更新:请参见末尾的注释)
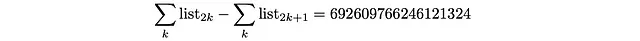
一种解决方法
奇数类别似乎人口过少(这是作者选择报告数据的近似的结果)。为了使事情正常运行(获得在范围[0,1]内的概率),我们决定将前面的大数字添加到深度类别21的人口中(这是人口最多的奇数类别,或者说是最不会注意到这种添加的类别)。通过这种修正,所有获得的概率似乎都是正确的(这意味着不等式也得到满足)。
跳跃概率如下:
p_i = {1., 0.916667, 0.903509, 0.903558, 0.903606, 0.903602, 0.90352, 0.903415, 0.903342, 0.903292, 0.903254, 0.903221, 0.903189, 0.903153, 0.903108, 0.903038, 0.902885, 0.902409, 0.900342, 0.889537, 0.818371, 0.367158, 0.00342857, 6.24863*1e-12, 0.00022, 0.0833333}# i从0到25q_i = {0.0833333, 0.0964912, 0.0964419, 0.096394, 0.0963981, 0.0964796, 0.096585, 0.096658, 0.0967081, 0.0967456, 0.0967786, 0.0968113, 0.0968467, 0.0968917, 0.0969625, 0.0971149, 0.0975908, 0.0996581, 0.110463, 0.181629, 0.632842, 0.996571, 1., 0.99978, 0.916667, 1.}# i从1到26请注意,几乎所有的第一个p_i(直到i = 21)都接近1.这些是离开解决状态的概率。对于大于21的 i ,靠近解决状态的概率q_i几乎为1。这解释了为什么解决魔方很困难:随机行走者(或魔方的随机移动者)将永远“被困在”深度类别21的邻域中。
p(d|N)
将p_i,q_i数值插入转移矩阵M中,马尔可夫过程完全被描述。特别地,如果我们从站点0以概率为1开始,经过N步,随机行走者将以概率处于站点d:
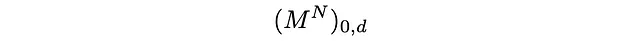
这是我们正在寻找的概率:
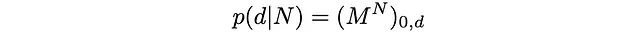
数值上,我们得知只有当N和d具有相同的奇偶性时,p(d|N)才不为零(这是一些鲁比克魔方研究者所熟知的)。下面我们绘制了一些不同N的p(d|N):
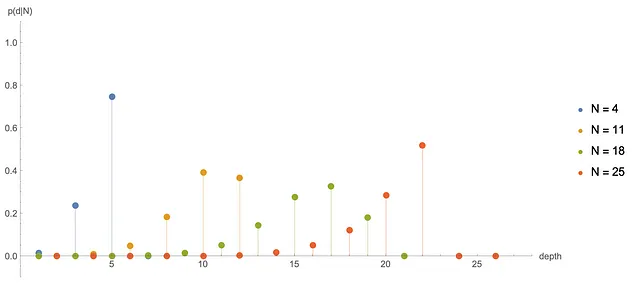
我们观察到在N = 31或32之后,p(d|N)与静止分布D(d)非常接近(除了在偶数和奇数位置之间来回切换)。这是关于多少步骤足以证明我们真正打乱魔方的另一个答案。
让我们注意到我们解决了一个逆问题。我们从静止分布获得了转移概率。对于一般的马尔可夫过程,这是不可能的。特别地,对于半转度量,使用这里描述的方法不可能找到p(d|N)。半转度量不同,因为我们可以在移动后保持在相同的深度类别(根据它们的移动定义)。这些自深度类别跳跃在转移矩阵的对角线上引入了额外的概率r_i,我们将有比方程更多的变量。
最后的评论
即使从计算的角度来看,魔方是一个需要35年的CPU问题,但它还有许多方面可以用分析或适度的数值方法描述。我们在这里计算的概率就是一个例子。我们所说的一切都可以轻松推广到更复杂的魔方衍生品。一个很酷的推广是转向更多维度:S = 4D、5D、6D等维度的魔方。在这些情况下,状态空间随着S的增加呈指数增长。因此,有些魔方的马尔可夫链长度可以任意长。换句话说,我们有类似的谜题,其上帝数可以任意大(粗略地说,上帝数是状态数的对数,而状态数随着维度的增加而增加)。在这些情况下,我们可以取某些极限,解释我们3D情况的某些方面,如下面这个:
在上帝数G很大的极限下,概率p(d|N)应该接近二项分布
不难看出为什么可能是这样。如果很大,D_d的指数增长对于大多数d来说将是非常稳定的。这是一个大胆但不过分疯狂的猜测:
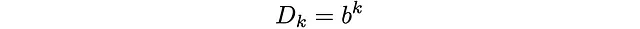
对于远离0和G的k。正如我们所说,在S = 3D情况下,b = 9.34。对于更高的S,b应该增加(拥有更多的面将增加分支因子b)。这导致了以下概率值:
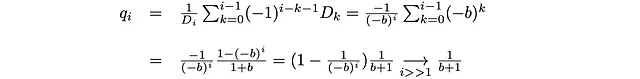
当i远离原点(i>>1)和上帝数(i<<G)时,q_i趋近于一个常数值1/(b+1)。在这个范围内,p_i也会是常数。你可以看到在3D情况下,i=3, …, 15的p_i和q_i的值几乎是常数,q_i约等于1/(b+1),其中b = 9.34。对于0 << i << G,我们将有一个具有恒定概率的一维随机行走者,向后(q)和向前(p)。在这种情况下,行走者的位置将由类似二项分布的分布描述。
在N次试验之后,随机行走者向右走k步(成功率p),向左走N-k步(成功率q)的概率是二项分布(Binomial(k,N,p))。然后,经过N步行走后所走的距离将会是
d = k – (N – k),
由此我们可以得到
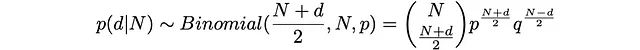
从这里我们可以得到对于最有可能的d的分析估计
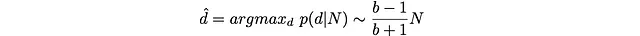
这很有趣:随着立方体的维度S的增加,分支因子b增加,最有可能的深度d实际上接近于N。
更新说明:在本故事发表后,我联系了Tomas Rokicki和Morley Davidson(2012年在半转角度度量中证明“上帝数字为20”的两位作者)关于他们所报告的D(d)和我使用它得到的负概率。他们与我分享了一组更准确的数据,包括深度d = 19,…,24的下限和上限。他们的数据与这里得到的不等式完全兼容,并且与偶数深度类别的人口应等于奇数深度类别的人口(在四分之一转角度量中)的事实相吻合。在使用这组新数据时,这里计算的概率有一个可以忽略的修正。