建模混沌系统
摆锤是我们都熟悉的经典物理系统。无论是大型悬挂钟还是摇摆的孩子,我们都见过摆锤的规律、周期性运动。单摆在经典物理中有明确定义,但双摆(将一个摆锤连接到另一个摆锤的末端)则是真正的混沌。在本文中,我们将在对摆锤的直观理解基础上建模双摆的混沌行为。这里的物理现象非常有趣,所需的数值方法是任何人必备的工具。
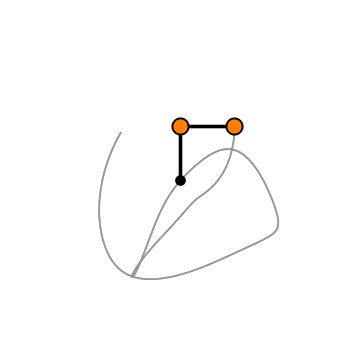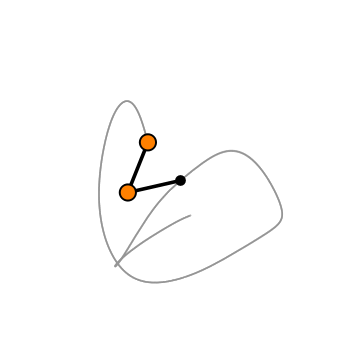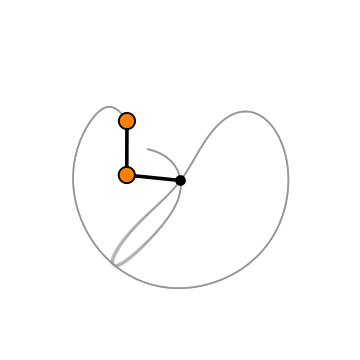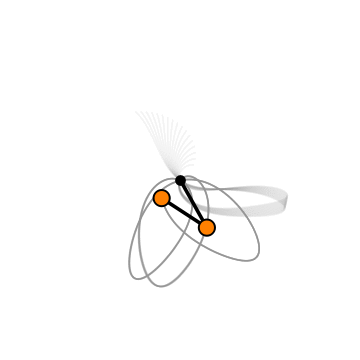
本文中,我们将:
- 了解谐振运动并建模单摆的行为
- 学习混沌理论的基础知识
- 使用数值方法来模拟双摆的混沌行为
谐振运动和单摆
简谐运动
我们将摆锤的周期性振动称为谐振运动。当系统中存在运动,并且该运动受到与该运动方向相反的成比例恢复力的平衡时,就会发生谐振运动。我们在图2中看到了一个例子,弹簧上的质量由于重力被拉下,但这会将能量传递给弹簧,然后弹簧弹回并将质量拉起。在弹簧系统旁边,我们可以看到质量的高度绕着一个叫做相量图的圆圈运动,进一步说明系统的规律运动。
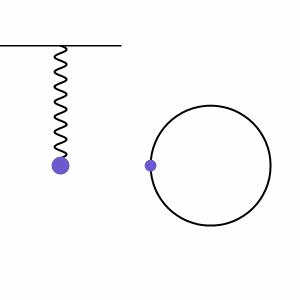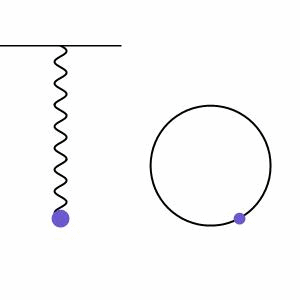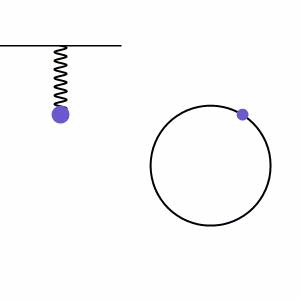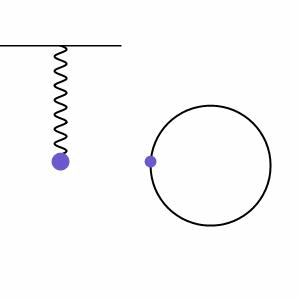
谐振运动可以是阻尼的(由于阻力而振幅逐渐减小)或驱动的(由于外力的作用而振幅逐渐增大),但我们将从没有外力作用的无限谐振运动的最简单情况开始(无阻尼运动)。这种运动方式很好地适用于模拟小角度/低振幅摆动的单摆。在这种情况下,我们可以使用下面的方程来模拟运动。

我们可以轻松地将这个函数编写为代码,并模拟一个简单摆。
def simple_pendulum(theta_0, omega, t, phi): theta = theta_0*np.cos(omega*t + phi) return theta#系统的参数theta_0 = np.radians(15) #角度转弧度g = 9.8 #m/s^2l = 1.0 #momega = np.sqrt(g/l)phi = 0 #对于小角度time_span = np.linspace(0,20,300) #模拟20秒,分成300个时间间隔theta = []for t in time_span: theta.append(simple_pendulum(theta_0, omega, t, phi))#转换为笛卡尔坐标x = l*np.sin(theta)y = -l*np.cos(theta) #取负号确保摆向下
使用拉格朗日力学的完整摆动运动
一个简单的小角度摆可以作为一个良好的起点,但我们想要超越这个,模拟一个完整的摆的运动。因为我们不能再使用小角度近似,所以最好使用Lagrange力学模型来描述摆的运动。这是物理学中的一个基本工具,它将我们从系统中的力转变为系统中的能量。我们将参考框架从驱动力与恢复力转变为动能与势能。
Lagrangian是动能与势能之差,由方程2给出。
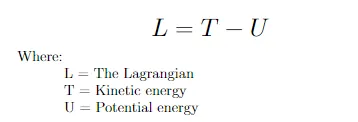
将方程3中给出的摆的动能和势能代入,得到方程4描述的摆的Lagrangian。
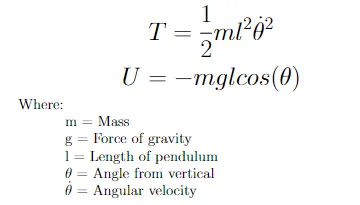
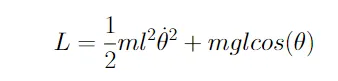
有了摆的Lagrangian,我们现在可以描述系统的能量。还有最后一步需要通过欧拉-拉格朗日方程将能量参考转换为动力学/力导向参考。使用这个方程,我们可以使用Lagrangian获取摆的角加速度。
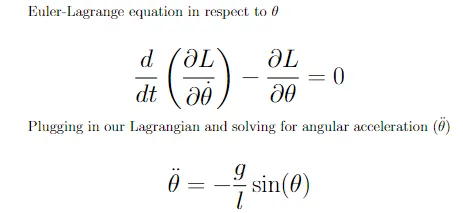
经过数学推导,我们得到了角加速度,可以用它来计算角速度和角度本身。这将需要一些数值积分,这将在我们的完整摆模拟中进行说明。即使对于单个摆,非线性动力学意味着没有解析解来求解θ,因此需要数值解。积分非常简单(但强大),我们使用角加速度更新角速度,使用角速度更新θ,将前者添加到后者并乘以一些时间步长。这给我们一个加速度/速度曲线下的面积的近似值。时间步长越小,近似值越准确。
def full_pendulum(g,l,theta,theta_velocity, time_step): #数值积分 theta_acceleration = -(g/l)*np.sin(theta) #得到加速度 theta_velocity += time_step*theta_acceleration #用加速度更新速度 theta += time_step*theta_velocity #用角速度更新角度 return theta, theta_velocityg = 9.8 #m/s^2l = 1.0 #mtheta = [np.radians(90)] #theta_0theta_velocity = 0 #初始速度为0time_step = 20/300 #定义一个时间步长time_span = np.linspace(0,20,300) #模拟20秒,分成300个时间间隔for t in time_span: theta_new, theta_velocity = full_pendulum(g,l,theta[-1], theta_velocity, time_step) theta.append(theta_new)#转换回笛卡尔坐标 x = l*np.sin(theta)y = -l*np.cos(theta)
我们已经模拟了一个完整的摆,但这仍然是一个明确定义的系统。现在是时候进入双摆的混沌世界了。
混沌与双摆
在数学意义上,混沌指的是对初始条件非常敏感的系统。即使是微小的系统起始变化也会导致系统行为的巨大差异。这完美地描述了双摆的运动。与单摆不同,双摆不是一个表现良好的系统,即使是轻微的起始角度变化也会导致系统以完全不同的方式演化。
为了模拟双摆的运动,我们将使用与之前相同的拉格朗日方法(见完整推导)。
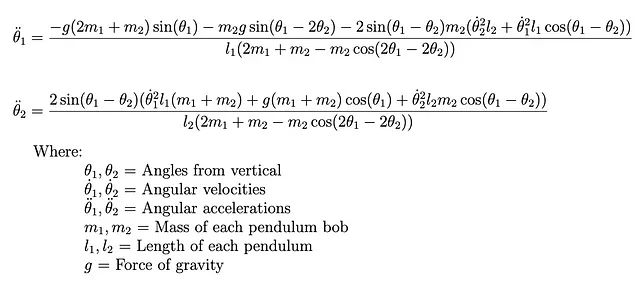
在将此方程实现为代码并找到θ时,我们将使用与之前相同的数值积分方案。
#获取θ1加速度def theta1_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g): mass1 = -g*(2*m1 + m2)*np.sin(theta1) mass2 = -m2*g*np.sin(theta1 - 2*theta2) interaction = -2*np.sin(theta1 - theta2)*m2*np.cos(theta2_velocity**2*l2 + theta1_velocity**2*l1*np.cos(theta1 - theta2)) normalization = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2)) theta1_ddot = (mass1 + mass2 + interaction)/normalization return theta1_ddot#获取θ2加速度def theta2_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g): system = 2*np.sin(theta1 - theta2)*(theta1_velocity**2*l1*(m1 + m2) + g*(m1 + m2)*np.cos(theta1) + theta2_velocity**2*l2*m2*np.cos(theta1 - theta2)) normalization = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2)) theta2_ddot = system/normalization return theta2_ddot#更新θ1def theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step): #数值积分 theta1_velocity += time_step*theta1_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g) theta1 += time_step*theta1_velocity return theta1, theta1_velocity#更新θ2def theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step): #数值积分 theta2_velocity += time_step*theta2_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g) theta2 += time_step*theta2_velocity return theta2, theta2_velocity#运行完整的双摆def double_pendulum(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step,time_span): theta1_list = [theta1] theta2_list = [theta2] for t in time_span: theta1, theta1_velocity = theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step) theta2, theta2_velocity = theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step) theta1_list.append(theta1) theta2_list.append(theta2) x1 = l1*np.sin(theta1_list) #摆1 x y1 = -l1*np.cos(theta1_list) #摆1 y x2 = l1*np.sin(theta1_list) + l2*np.sin(theta2_list) #摆2 x y2 = -l1*np.cos(theta1_list) - l2*np.cos(theta2_list) #摆2 y return x1,y1,x2,y2
#定义系统参数g = 9.8 #m/s^2m1 = 1 #kgm2 = 1 #kgl1 = 1 #ml2 = 1 #mtheta1 = np.radians(90)theta2 = np.radians(45)theta1_velocity = 0 #m/stheta2_velocity = 0 #m/stheta1_list = [theta1]theta2_list = [theta2]time_step = 20/300time_span = np.linspace(0,20,300)x1,y1,x2,y2 = double_pendulum(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step,time_span)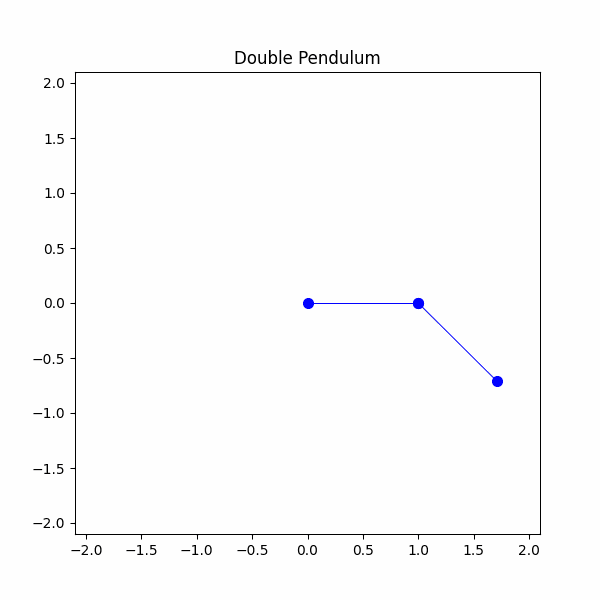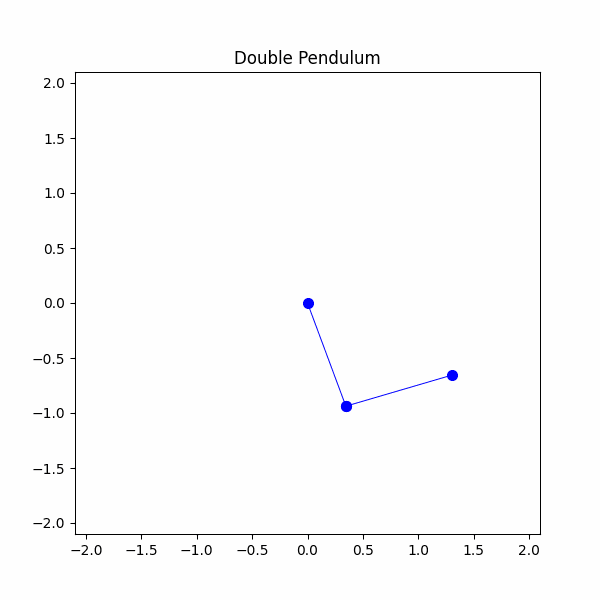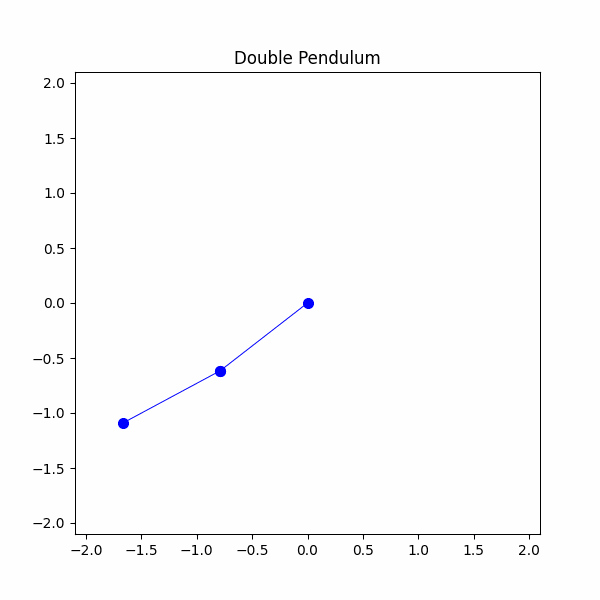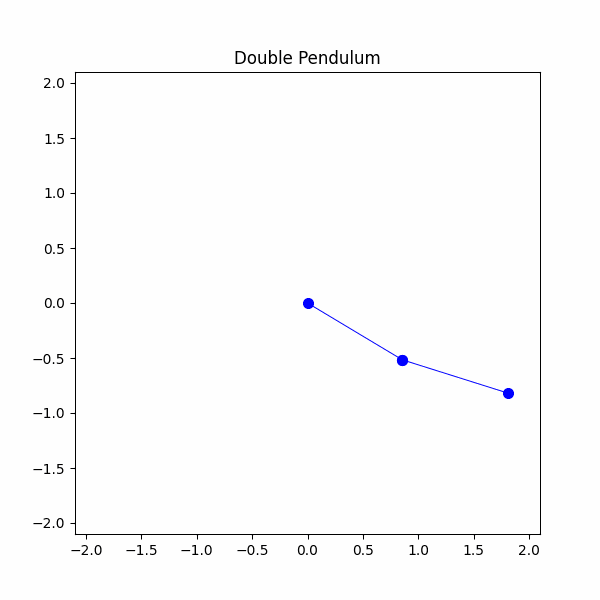
我们终于做到了!我们成功地建模了一个双摆,现在是观察一些混沌的时候了。我们最终的模拟将是两个具有稍微不同起始条件的双摆。我们将设置一个摆角1为90度,另一个摆角1为91度。让我们看看会发生什么。
我们可以看到,两个摆的初始轨迹相似,但很快就开始发散。这就是我们所说的混沌,即使角度相差1度,也会导致完全不同的最终行为。
结论
在本文中,我们学习了关于摆动运动及其建模的知识。我们从最简单的谐振运动模型开始,逐步发展到复杂且混沌的双摆模型。在此过程中,我们了解了拉格朗日方程、混沌和数值积分的知识。
双摆是混沌系统的最简单示例。这些系统存在于我们的世界的各个领域,包括人口动态、气候甚至台球。我们可以从双摆中学到的教训,并在遇到混沌系统时加以应用。
要点
- 混沌系统对初始条件非常敏感,在起始条件稍微改变时,它们的演变方式会发生巨大变化。
- 在处理一个系统,尤其是混沌系统时,是否有另一个参考系可以使其更容易处理?(例如,从力参考系转换到能量参考系)
- 当系统变得过于复杂时,我们需要实施数值解来解决问题。这些解法简单而强大,并提供了对实际行为的良好近似。
参考资料
本文中使用的所有图均由作者创建或来自Math Images,并遵循GNU Free Documentation License 1.2
一切都是谐振子
物理学本科生可能开玩笑说宇宙是由谐振子构成的,但他们并不离谱。
www.wired.com
经典力学,约翰·泰勒 https://neuroself.files.wordpress.com/2020/09/taylor-2005-classical-mechanics.pdf
完整代码
简单摆
def makeGif(x,y,name): !mkdir frames counter=0 images = [] for i in range(0,len(x)): plt.figure(figsize = (6,6)) plt.plot([0,x[i]],[0,y[i]], "o-", color = "b", markersize = 7, linewidth=.7 ) plt.title("Pendulum") plt.xlim(-1.1,1.1) plt.ylim(-1.1,1.1) plt.savefig("frames/" + str(counter)+ ".png") images.append(imageio.imread("frames/" + str(counter)+ ".png")) counter += 1 plt.close() imageio.mimsave(name, images) !rm -r framesdef simple_pendulum(theta_0, omega, t, phi): theta = theta_0*np.cos(omega*t + phi) return theta#parameters of our systemtheta_0 = np.radians(15) #degrees to radiansg = 9.8 #m/s^2l = 1.0 #momega = np.sqrt(g/l)phi = 0 #for small angletime_span = np.linspace(0,20,300) #simulate for 20s split into 300 time intervalstheta = []for t in time_span: theta.append(simple_pendulum(theta_0, omega, t, phi))x = l*np.sin(theta)y = -l*np.cos(theta) #negative to make sure the pendulum is facing down摆锤
def full_pendulum(g,l,theta,theta_velocity, time_step): theta_acceleration = -(g/l)*np.sin(theta) theta_velocity += time_step*theta_acceleration theta += time_step*theta_velocity return theta, theta_velocityg = 9.8 #m/s^2l = 1.0 #mtheta = [np.radians(90)] #theta_0theta_velocity = 0time_step = 20/300time_span = np.linspace(0,20,300) #模拟20秒,分成300个时间间隔for t in time_span: theta_new, theta_velocity = full_pendulum(g,l,theta[-1], theta_velocity, time_step) theta.append(theta_new)#转回笛卡尔坐标 x = l*np.sin(theta)y = -l*np.cos(theta)#使用简单摆函数makeGif(x,y,"pendulum.gif")双摆
def theta1_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g): mass1 = -g*(2*m1 + m2)*np.sin(theta1) mass2 = -m2*g*np.sin(theta1 - 2*theta2) interaction = -2*np.sin(theta1 - theta2)*m2*np.cos(theta2_velocity**2*l2 + theta1_velocity**2*l1*np.cos(theta1 - theta2)) normalization = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2)) theta1_ddot = (mass1 + mass2 + interaction)/normalization return theta1_ddotdef theta2_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g): system = 2*np.sin(theta1 - theta2)*(theta1_velocity**2*l1*(m1 + m2) + g*(m1 + m2)*np.cos(theta1) + theta2_velocity**2*l2*m2*np.cos(theta1 - theta2)) normalization = l1*(2*m1 + m2 - m2*np.cos(2*theta1 - 2*theta2)) theta2_ddot = system/normalization return theta2_ddotdef theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step): theta1_velocity += time_step*theta1_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g) theta1 += time_step*theta1_velocity return theta1, theta1_velocitydef theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step): theta2_velocity += time_step*theta2_acceleration(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g) theta2 += time_step*theta2_velocity return theta2, theta2_velocitydef double_pendulum(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step,time_span): theta1_list = [theta1] theta2_list = [theta2] for t in time_span: theta1, theta1_velocity = theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step) theta2, theta2_velocity = theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step) theta1_list.append(theta1) theta2_list.append(theta2) x1 = l1*np.sin(theta1_list) y1 = -l1*np.cos(theta1_list) x2 = l1*np.sin(theta1_list) + l2*np.sin(theta2_list) y2 = -l1*np.cos(theta1_list) - l2*np.cos(theta2_list) return x1,y1,x2,y2
#定义系统参数,运行双摆g = 9.8 #m/s^2m1 = 1 #kgm2 = 1 #kgl1 = 1 #ml2 = 1 #mtheta1 = np.radians(90)theta2 = np.radians(45)theta1_velocity = 0 #m/stheta2_velocity = 0 #m/stheta1_list = [theta1]theta2_list = [theta2]time_step = 20/300time_span = np.linspace(0,20,300)for t in time_span: theta1, theta1_velocity = theta1_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step) theta2, theta2_velocity = theta2_update(m1,m2,l1,l2,theta1,theta2,theta1_velocity,theta2_velocity,g,time_step) theta1_list.append(theta1) theta2_list.append(theta2) x1 = l1*np.sin(theta1_list)y1 = -l1*np.cos(theta1_list)x2 = l1*np.sin(theta1_list) + l2*np.sin(theta2_list)y2 = -l1*np.cos(theta1_list) - l2*np.cos(theta2_list)
#制作gif文件!mkdir frames counter=0images = []for i in range(0,len(x1)): plt.figure(figsize = (6,6)) plt.figure(figsize = (6,6)) plt.plot([0,x1[i]],[0,y1[i]], "o-", color = "b", markersize = 7, linewidth=.7 ) plt.plot([x1[i],x2[i]],[y1[i],y2[i]], "o-", color = "b", markersize = 7, linewidth=.7 ) plt.title("双摆") plt.xlim(-2.1,2.1) plt.ylim(-2.1,2.1) plt.savefig("frames/" + str(counter)+ ".png") images.append(imageio.imread("frames/" + str(counter)+ ".png")) counter += 1 plt.close()imageio.mimsave("double_pendulum.gif", images)!rm -r frames