了解如何将分治范式应用于排序

介绍
在排序方面,归并排序是最流行的算法之一。它基于著名的“分治”范式,将一个大问题分解为更容易解决的小问题,然后将它们的解决方案合并为原始问题的解决方案。
在本教程中,我们将深入研究实现细节,并以大O表示法估计归并排序的复杂度。为了更好地理解,我们还将提供一个示例。
算法
该算法的思想是递归地对原始数组的较小子数组进行排序。当多个子数组排序完成后,它们会转换为一个更大尺寸的新数组。这个过程会一直持续,直到我们得到初始数组的排序版本。
起初,这可能看起来太复杂了,但事实证明,基于已排序数组的新排序数组的获取是一个相对快速的过程。
我们将从查看合并函数开始。然后,我们将将其用于算法的最终版本。
合并函数
合并函数接受两个已排序的子数组,并返回由这两个子数组的元素组成的新排序数组。在下面的代码片段中,一个元素数组与两个已排序的子数组 array[left, middle] 和 array[middle + 1, right] 一起传递。
合并函数
我们使用两个指针 i 和 j 来循环遍历两个数组的元素。通过在每次迭代中比较 array[i] 和 array[j] 的元素,我们将较小的元素添加到 new_array 中。随后,根据添加的元素,增加指针 i 或 j,使其指向下一个元素。
循环会一直持续,直到要么一个子数组的所有元素都添加到了 new_array 中,要么另一个子数组的较大值元素都添加完毕。
最后,我们将排序后的 new_array 的每个元素复制到原始数组中。因此,数组中从索引 left 到 right 的所有元素都是排序好的。
需要注意的是,对于长度为 N 的两个子数组,我们只需线性地遍历每个元素一次。这导致该方法的复杂度为 O(N)。
合并示例
假设我们有一个由两个已排序子数组 array[0:3] 和 array[4:7] 组成的数组。首先,我们初始化两个指针 i 和 j,它们指向最小的元素。在我们的例子中,它们分别指向索引为 0 和 4 的元素。
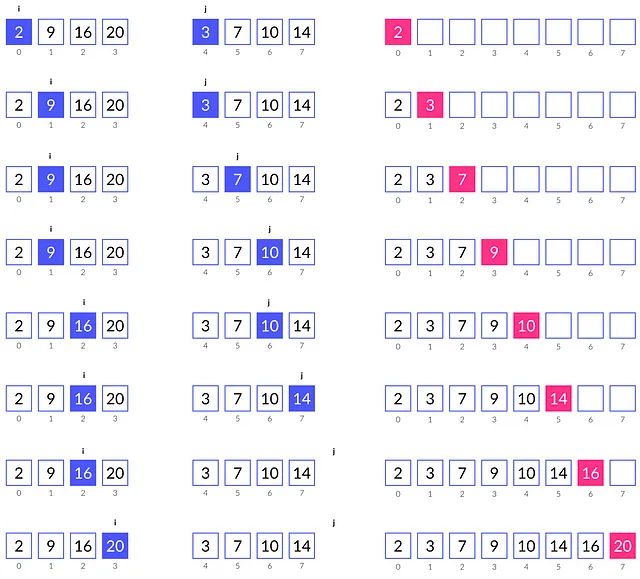
迭代 1。我们比较 array[0] = 2 和 array[4] = 3。由于 2 ≤ 3,我们将 2 保存为新数组的第一个元素,并将 i 增加 1,使其指向下一个递增的元素,即 9。
迭代 2。我们比较 array[1] = 9 和 array[4] = 3。由于 9 > 3,我们将 3 保存为新数组的第二个元素,并将 j 增加 1,使其指向下一个递增的元素,即 7。
迭代 3。array[1] = 9 > array[5] = 7。我们将 7 保存为下一个元素。j 增加了 1。
…
迭代 7。j 指向右侧数组的末尾。这意味着左侧数组中索引 i 开始的所有元素都大于右侧数组中的任何元素。因此,我们将右侧数组中剩下的所有元素(16 和 20)复制到新数组中。
完成此过程后,所有排序后的新数组的值将被复制到原始数组中。
排序函数
排序函数递归地调用自身,分别对其左半部分和右半部分进行排序。当两个半部分都排序完成后,它们在 merge_sort() 函数调用后进行合并。
归并排序函数
为了使客户端更方便地使用函数接口,可以将 merge_sort() 的第一次函数调用包装在另一个函数中。这样客户端就不需要传递函数的左半部分和右半部分参数,这符合封装设计原则。
将归并排序调用封装到另一个函数中
示例
下图显示了对包含 8 个元素的数组进行归并排序的层次调用。首先,我们将数组分成两个长度为 4 的相等部分。对于每个部分,我们再次调用归并排序。这将得到长度为 2 的数组。顺便说一下,不需要再次将这些数组分割,因为任何由单个元素组成的数组都是已经排序的。

我们通过对长度为 2 的数组进行排序来继续算法。一旦两个连续的长度为 2 的数组排序完成,它们将合并成一个新的长度为 4 的已排序数组。这个过程对所有长度为 2 的数组都进行。一旦两个连续的长度为 4 的数组排序完成,它们将类似地合并成一个新的长度为 8 的已排序数组。
当所有元素都排序完成时,我们终止该过程。
复杂度
为了评估复杂度,我们首先需要了解递归调用的结构。假设我们有一个需要排序的大小为 N 的数组。
我们将该数组分成大小为 N / 2 的两个部分。这两个部分又分别分成大小为 N / 4 的两个更小的部分。因此,我们最终得到了大小为 N / 4 的 4 个数组。类似地,在下一级中,我们得到了大小为 N / 8 的 8 个数组。我们继续这个过程,直到得到大小为 1 的 N 个数组。这个过程在下图中说明。
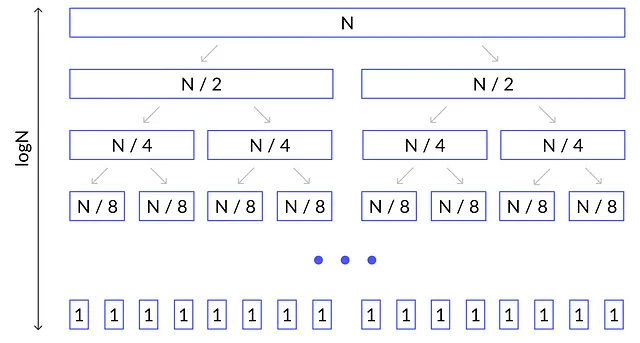
对于上图中的每个数组,我们需要调用一个归并过程,该过程需要 O(K) 的时间,其中 K 是数组的长度。让我们计算上图中每个级别的总时间复杂度。
- 对于第一级,我们有一个大小为 N 的数组,需要 O(N) 的处理时间。
- 对于第二级,我们有大小为 N / 2 的 2 个数组。每个数组需要 O(N / 2) 的时间。总时间是 2 * O(N / 2) = O(N)。
- 对于第三级,我们有大小为 N / 4 的 4 个数组。每个数组需要 O(N / 4) 的时间。总时间是 4 * O(N / 2) = O(N)。
- 最后一级包含 N 个大小为 1 的数组。每个数组需要 O(1) 的时间。总时间是 N * O(1) = O(N)。
按照这个逻辑,很明显每个级别需要 O(N) 的处理时间。由于每个数组在每一步都被分成两半,很容易注意到存在 O(logN) 个级别。这导致最终的时间复杂度为 O(N) * O(logN) = O(N * logN)。
优势
- 高效性。归并排序的总体复杂度为 O(N * logN)。这是基于比较数组元素的所有排序算法中最好的复杂度。然而,在合并过程中,需要将元素临时排序在另一个数组中。这个数组的大小与两个子数组的长度相同,因此需要 O(N) 的内存空间。
- 简单性。与其他高效的排序算法相比,归并排序可以更容易地解释和实现。
- 稳定排序。如果初始数组具有相等的元素,则归并排序算法不会改变它们的相对位置。这是一个重要的属性,被更复杂的算法在实现中使用到具有排序部分的情况。
结论
我们已经了解了其中一种最受欢迎的排序算法,它帮助我们理解了分治范式的原理。除此之外,归并排序巧妙地将简单性与高效复杂度相结合,并应用于大量的应用中。
除非另有注明,所有图片均为作者所创作。