给定函数的图形的可微性

考虑以下函数：

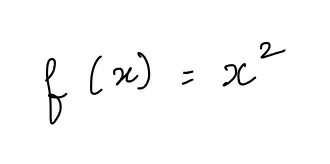
它的图像为：

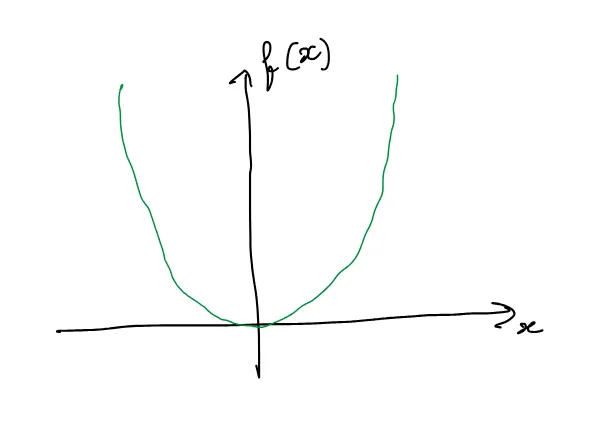
函数在某点的导数是该点处切线的斜率。对于这个函数，在其定义域中的所有点x处都存在导数。但是，并不是所有函数都是如此。有些函数在其定义域的所有点处都没有导数。在本文中，我们将看到函数不具有导数的三种类型的点；也就是说，它们是不可微的。

如果一个函数的导数在其定义域中的所有点x处存在，则该函数被正式定义为可微的。也就是说，如果你可以在其定义域中的每个点计算出一个唯一的值，那么它被称为可微的。

如果你可以在不从纸上抬起铅笔的情况下绘制出函数的图像，则该函数被认为是连续的。

让我们考虑函数f(x) = |x|。它的定义为：

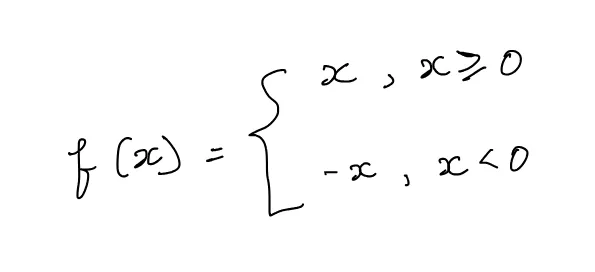
它的图像绘制如下：

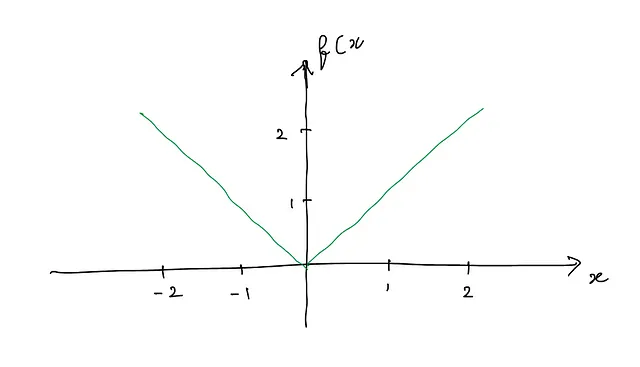
这是一个连续函数。让我们在x = 0处绘制一个切线。它可以绘制为（红线是切线）：

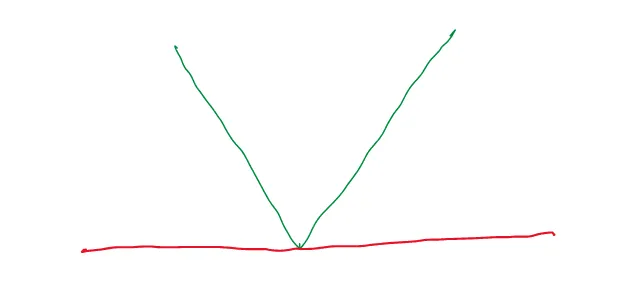
但是，也可以在x = 0处绘制另一条切线：

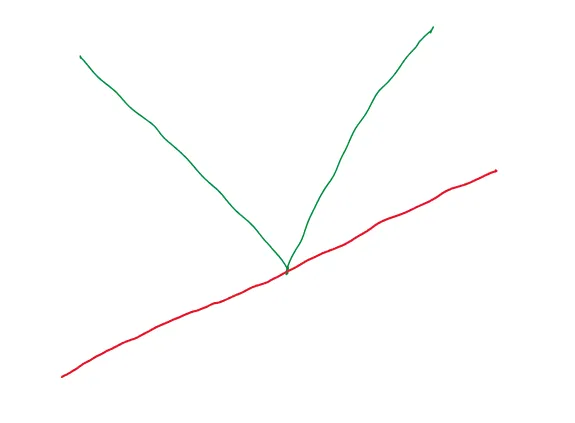
这条线只在一个点上与函数相切，即x = 0。所以，它确实是一条切线。实际上，对于这个函数，在x = 0处可能有多条这样的切线：

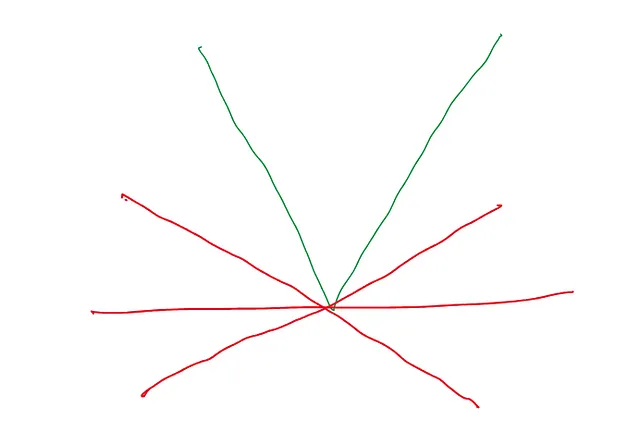
这意味着在x = 0处切线的斜率没有唯一的值。

让我们也来看看极限计算。

f(x)的导数被定义为以下极限的值：

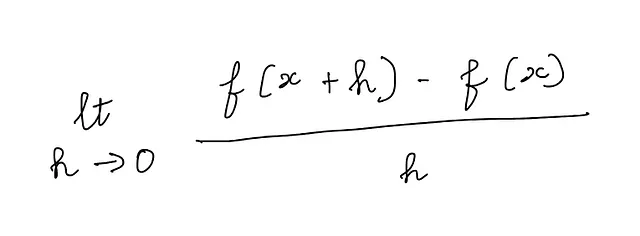
我们来计算一侧的极限：

左极限：

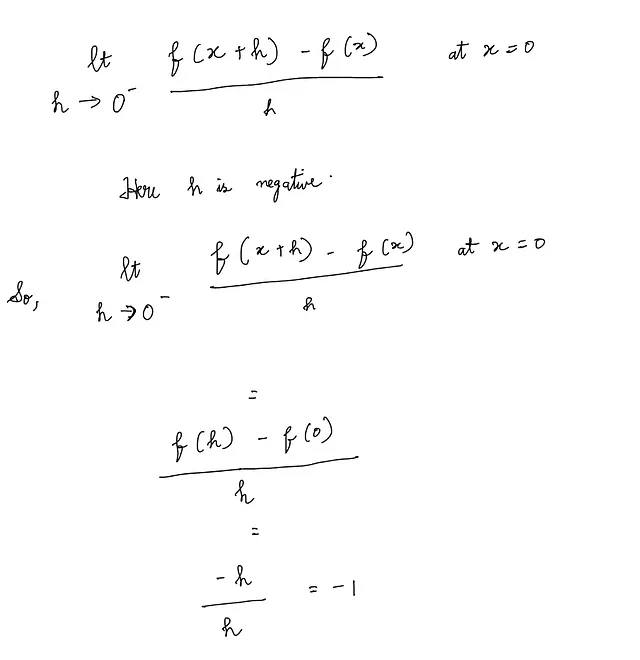
右极限：

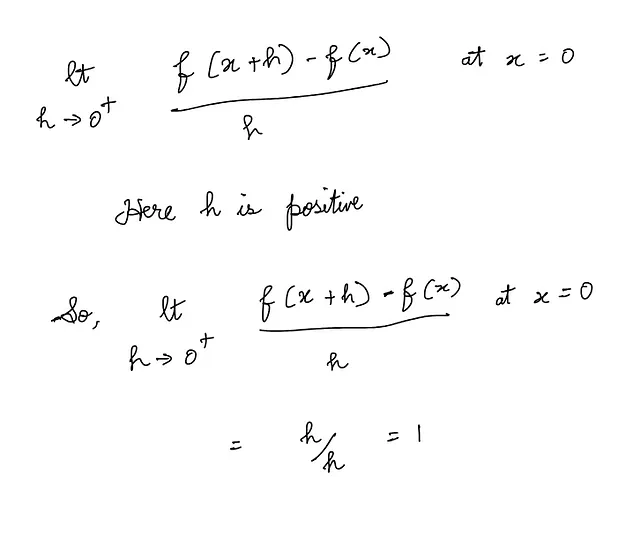
左极限为-1，右极限为1。它们不一致。所以，极限没有唯一的值，因此不存在。因此，f(x) = |x|在x = 0处不可微。这种函数被称为有一个角点（也称为尖点或转折点）。这样的函数是非光滑的。一个这样函数的示例图像如下：

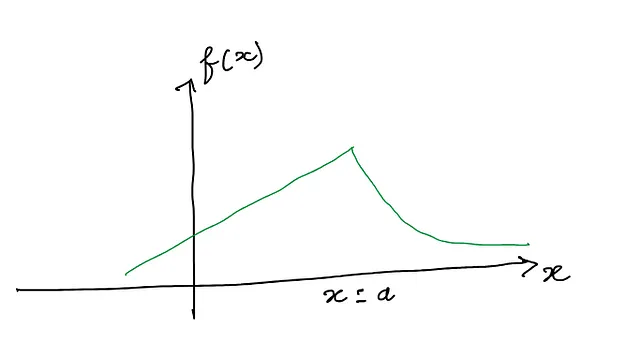
这个函数在x=a处有一个拐点。

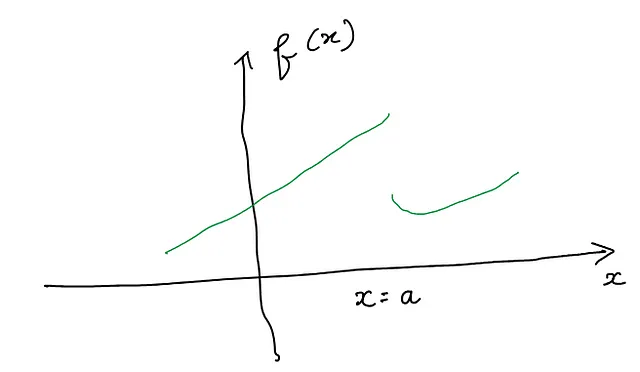
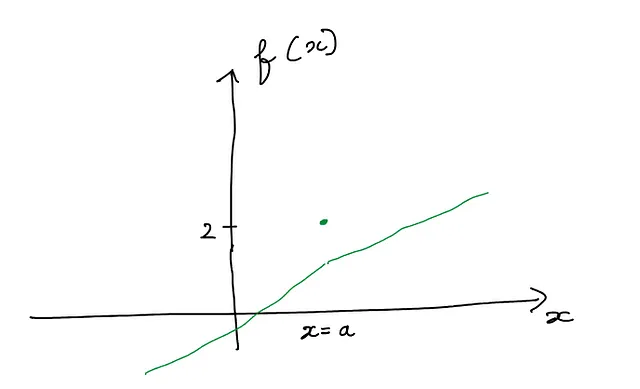
如下所示的不连续函数在不连续点也是不可微的，因为左右极限不相等：

注意：

1. 函数取无穷大值的点也被称为不连续点。
2. 当函数的值是一个单点值时，也是一个不连续点，如下图所示。这个函数在x=a处的单点值为2：

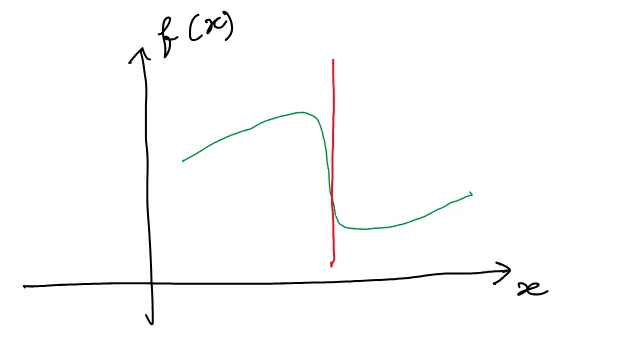
当切线是垂直的时，函数在该点是不可微的，因为在该点切线的斜率未定义（无穷大）。下面是一个示例（红线是x=a处的切线）：

因此，函数不可微的点有三种类型：

1. 拐角（或尖点）
2. 不连续点（跳跃、无穷大、单点）
3. 垂直切线（斜率未定义）

以下函数在哪些点是不可微的？

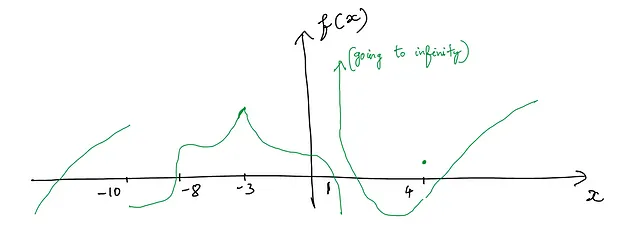
这些点是：

1. 拐角 -> -3
2. 不连续点 -> -10, 1, 4
3. 垂直切线 -> -8